Ergodic Process

ERGODIC PROCESS:

In the event that the distributions and statistics are not available we can avail ourselves of the time averages from the particular sample function. The mean of the sample function Xλo(t) is referred to as the sample mean of the process X(t) and is defined as

This quantity is actually a random-variable by itself because its value depends on the parameter sample function over it was calculated. the sample variance of the random process is defined as

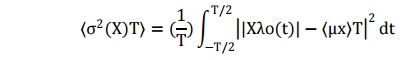
The time-averaged sample ACF is obtained via the relation is

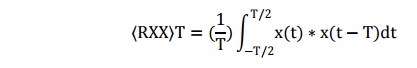
These quantities are in general not the same as the ensemble averages described before. A random process X(t) is said to be ergodic in the mean, i.e., first-order ergodic if the mean of sample average asymptotically approaches the ensemble mean

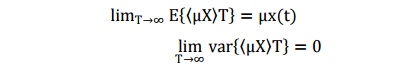
In a similar sense a random process X(t) is said to be ergodic in the ACF, i.e, second-order ergodic if

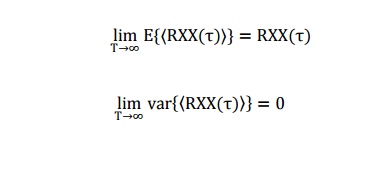
The concept of ergodicity is also significant from a measurement perspective because in Practical situations we do not have access to all the sample realizations of a random process. We therefore have to be content in these situations with the time-averages that we obtain from a single realization. Ergodic processes are signals for which measurements based on a single sample function are sufficient to determine the ensemble statistics. Random signal for which this property does not hold are referred to as non-ergodic processes. As before the Gaussian random signal is an exception where strict sense ergodicity implies wide sense ergodicity.