Global Code Scheduling

Global Code Scheduling

1 Primitive Code Motion

2 Upward Code Motion

3 Downward Code Motion

4 Updating Data Dependences

5 Global Scheduling Algorithms

6 Advanced Code Motion Techniques

7 Interaction with Dynamic Schedulers

8 Exercises for Section 10.4

For a machine with a moderate amount of instruction-level parallelism, sched-ules created by compacting individual basic blocks tend to leave many resources idle. In order to make better use of machine resources, it is necessary to con-sider code-generation strategies that move instructions from one basic block to another. Strategies that consider more than one basic block at a time are referred to as global scheduling algorithms. To do global scheduling correctly, we must consider not only data dependences but also control dependences. We must ensure that

1.           All instructions in the original program are executed in the optimized program, and

2.           While the optimized program may execute extra instructions speculatively, these instructions must not have any unwanted side effects.

1. Primitive Code Motion

Let us first study the issues involved in moving operations around by way of a simple example.

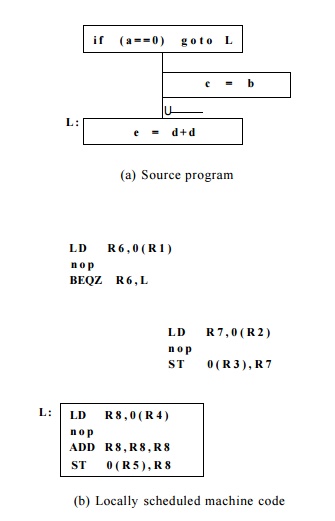
E x a m p l e 1 0 . 9 : Suppose we have a machine that can execute any two oper-ations in a single clock. Every operation executes with a delay of one clock, except for the load operation, which has a latency of two clocks. For simplicity, we assume that all memory accesses in the example are valid and will hit in the cache. Figure 10.12(a) shows a simple flow graph with three basic blocks. The code is expanded into machine operations in Figure 10.12(b). All the instruc-tions in each basic block must execute serially because of data dependences; in fact, a no-op instruction has to be inserted in every basic block.

Assume that the addresses of variables a, b, c, d, and e are distinct and that those addresses are stored in registers Rl through R5, respectively. The com-putations from different basic blocks therefore share no data dependences. We observe that all the operations in block B₃ are executed regardless of whether the branch is taken, and can therefore be executed in parallel with operations from block B1. We cannot move operations from B1 down to B₃, because they are needed to determine the outcome of the branch.

Operations in block B₂ are control-dependent on the test in block B1. We can perform the load from B₂ speculatively in block B1 for free and shave two clocks from the execution time whenever the branch is taken.

Stores  should  not  be  performed speculatively because they  overwrite the old value in a memory location.  It is possible, however, to delay a store operation. We cannot simply place the store operation from block B2 in block B3, because it should only be executed if the flow of control passes through block B2. However, we can place the store operation in a duplicated copy of B3. Figure 10.12(c) shows such an optimized schedule. The optimized code executes in 4 clocks, which is the same as the time it takes to execute B3 alone.

Example  10.9 shows that it is possible to move operations up  and down an execution path.  Every pair of basic blocks in this example has a different "dominance relation," and thus the considerations of when and how instructions can be moved between each pair are different.  As discussed in Section 9.6.1, a block B  is said to  dominate block B'  if every path from the  entry of the control-flow graph to  B'  goes through  B. Similarly,  a block  B  postdominates block B' if every path from B' to the exit of the graph goes through B.  When B dominates B' and B' postdominates B, we say that B and B' are control equivalent, meaning that one is executed when and only when the other is. For the example in Fig. 10.12, assuming Bx is the entry and B3 the exit,

1. B1 and B3    are control equivalent:  Bx    dominates B3    and B3    postdominates  Bi,

2. Bi  dominates B2    but  B2     does not postdominate B1,  and

3.  B₂    does not dominate B₃    but  B₃    postdominates B₂.

It is also possible for a pair of blocks along a path to share neither a dominance nor postdominance relation.

2. Upward Code Motion

We now examine carefully what it means to move an operation up a path. Suppose we wish to move an operation from block src up a control-flow path to block dst. We assume that such a move does not violate any data dependences and that it makes paths through dst and src run faster. If dst dominates src, and src postdominates dst, then the operation moved is executed once and only once, when it should.

If src  does  not  post dominate  dst

Then there exists a path that passes through dst that does not reach src. An extra operation would have been executed in this case. This code motion is illegal unless the operation moved has no unwanted side effects. If the moved operation executes "for free" (i.e., it uses only resources that otherwise would be idle), then this move has no cost. It is beneficial only if the control flow reaches src.

If dst does  not  dominate  src

Then there exists a path that reaches src without first going through dst.  We need to insert copies of the moved operation along such paths.  We know how to achieve exactly that from our discussion of partial redundancy elimination in Section 9.5-  We place copies of the operation along basic blocks that form a cut set separating the entry block from src.  At each place where the operation

is inserted, the following constraints must be satisfied:

1. The operands of the operation must hold the same values as in the original,

2.                 The result does not overwrite a value that is still needed, and

3.                 It itself is not subsequently overwritten befpre reaching src.

These copies render the original instruction in src fully redundant, and it thus can be eliminated.

We refer to the extra copies of the operation as compensation code. As dis-cussed in Section 9.5, basic blocks can be inserted along critical edges to create places for holding such copies. The compensation code can potentially make some paths run slower. Thus, this code motion improves program execution only if the optimized paths are executed more frequently than the nonopti-mized ones.

3. Downward Code Motion

Suppose we are interested in moving an operation from block src down a control-flow path to block dst. We can reason about such code motion in the same way as above.

If src does not dominate dst Then there exists a path that reaches  dst without first visiting src.  Again, an extra operation will be executed in this case. Unfortunately, downward code motion is often applied to writes, which have the side effects of overwriting old values. We can get around this problem by replicating the basic blocks along the paths from src to dst, and placing the operation only in the new copy of dst. Another approach, if available, is to use predicated instructions. We guard the operation moved with the predicate that guards the src block. Note that the predicated instruction must be scheduled only in a block dominated by the computation of the predicate, because the predicate would not be available otherwise.

If dst does  not  post dominate  src

As in the discussion above, compensation code needs to be inserted so that the operation moved is executed on all paths not visiting dst. This transformation is again analogous to partial redundancy elimination, except that the copies are placed below the src block in a cut set that separates src from the exit.

Summary of Upward  and  Downward  Code  Motion

From this discussion, we see that there is a range of possible global code mo-tions which vary in terms of benefit, cost, and implementation complexity. Fig-ure 10.13 shows a summary of these various code motions; the lines correspond to the following four cases:

1. Moving instructions between control-equivalent blocks is simplest and most cost effective. No extra operations are ever executed and no com-pensation code is needed.

2.                 Extra operations may be executed if the source does not postdominate (dominate) the destination in upward (downward) code motion. This code motion is beneficial if the extra operations can be executed for free, and the path passing through the source block is executed.

3.                 Compensation code is needed if the destination does not dominate (post-dominate) the source in upward (downward) code motion. The paths with the compensation code may be slowed down, so it is important that the optimized paths are more frequently executed.

4.                 The last case combines the disadvantages of the second and third case: extra operations may be executed and compensation code is needed.

4. Updating Data Dependences

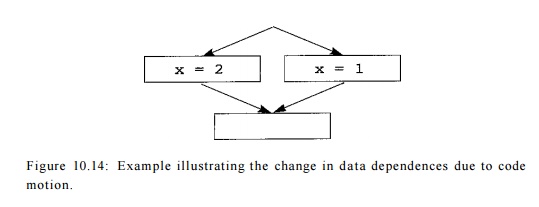
As illustrated by Example 10.10 below, dcode motion can change the data-Thus  dependence relations between operations. updated  data dependences must be after each code movement.

E x a m p l e 10 . 10 : For the flow graph shown in Fig. 10.14, either assignment to x can be moved up to the top block, since all the dependences in the original program are preserved with this transformation. However, once we have moved one assignment up, we cannot move the other. More specifically, we see that variable x is not live on exit in the top block before the code motion, but it is live after the motion. If a variable is live at a program point, then we cannot move speculative definitions to the variable above that program point.

5. Global Scheduling Algorithms

We saw in the last section that code motion can benefit some paths while hurting the performance of others. The good news is that instructions are not all created equal. In fact, it is well established that over 90% of a program's execution time is spent on less than 10% of the code. Thus, we should aim to make the frequently executed paths run faster while possibly making the less frequent paths run slower.

There are a number of techniques a compiler can use to estimate execution frequencies. It is reasonable to assume that instructions in the innermost loops are executed more often than code in outer loops, and that branches that go backward are more likely to be taken than not taken. Also, branch statements found to guard program exits or exception-handling routines are unlikely to be taken. The best frequency estimates, however, come from dynamic profiling. In this technique, programs are instrumented to record the outcomes of conditional branches as they run. The programs are then run on representative inputs to determine how they are likely to behave in general. The results obtained from this technique have been found to be quite accurate. Such information can be fed back to the compiler to use in its optimizations.

R e g i o n - B a s e d  S c h e d u l i n g

We now describe a straightforward global scheduler that supports the two eas-iest forms of code motion:

1.                 Moving operations up to control-equivalent basic blocks, and

2.                 Moving operations speculatively up one branch to a dominating predeces-sor.

Recall from Section 9.7.1 that a region is a subset of a control-flow graph that can be reached only through one entry block. We may represent any procedure as a hierarchy of regions. The entire procedure constitutes the top-level region, nested in it are subregions representing the natural loops in the function. We assume that the control-flow graph is reducible.

Algorithm 1 0 . 1 1 :  Region-based scheduling.

INPUT : A control-flow graph and a machine-resource description.

OUTPUT : A schedule S mapping each instruction to a basic block and a time slot.

METHOD : Execute the program in Fig. 10.15. Some shorthand terminology should  be  apparent: ControlEquiv(B)  is the  set of blocks that  are control- equivalent to block B,  and DominatedSucc applied to a set of blocks is the set of blocks that are successors of at least one block in the set and are dominated by all.    

Code scheduling in Algorithm  10.11 proceeds from the innermost regions to the outermost. When scheduling a region, each nested subregion is treated as a black box; instructions are not allowed to move in or out of a subregion. They can, however, move around a subregion, provided their data and control dependences are satisfied.

All control and dependence edges flowing back to the header of the region are ignored, so the resulting control-flow and data-dependence graphs are acyclic. The basic blocks in each region are visited in topological order. This ordering guarantees that a basic block is not scheduled until all the instructions it de-pends on have been scheduled. Instructions to be scheduled in a basic block B are drawn from all the blocks that are control-equivalent to B (including B), as well as their immediate successors that are dominated by B.

A list-scheduling algorithm is used to create the schedule for each basic block. The algorithm keeps a list of candidate instructions, Candlnsts, which contains all the instructions in the candidate blocks whose predecessors all have been scheduled. It creates the schedule clock-by-clock. For each clock, it checks each instruction from the Candlnsts in priority order and schedules it in that clock if resources permit. Algorithm 10.11 then updates Candlnsts and repeats the process, until all instructions from B are scheduled.

The priority order of instructions in Candlnsts uses a priority function sim-ilar to that discussed in Section 10.3. We make one important modification, however. We give instructions from blocks that are control equivalent to B higher priority than those from the successor blocks. The reason is that in-structions in the latter category are only speculatively executed in block B.

Loop  Unrolling

In region-based scheduling, the boundary of a loop iteration is a barrier to code motion. Operations from one iteration cannot overlap with those from another. One simple but highly effective technique to mitigate this problem is to unroll the loop a small number of times before code scheduling. A for-loop such as

can be written as in Fig. 10.16(b). Unrolling creates more instructions in the loop body, permitting global scheduling algorithms to find more parallelism.

Neighborhood  Compaction

Algorithm 10.11 only supports the first two forms of code motion described in Section 10.4.1. Code motions that require the introduction of compensation code can sometimes be useful. One way to support such code motions is to follow the region-based scheduling with a simple pass. In this pass, we can examine each pair of basic blocks that are executed one after the other, and check if any operation  can be moved up  or down  between them to improve the execution time of those blocks.  If such a pair is found, we check if the instruction to be moved needs to be duplicated along other paths. The code motion is made if it results in an expected net gain.

This simple extension can be quite effective in improving the performance of loops. For instance, it can move an operation at the beginning of one iteration to the end of the preceding iteration, while also moving the operation from the first iteration out of the loop. This optimization is particularly attractive for tight loops, which are loops that execute only a few instructions per iteration. However, the impact of this technique is limited by the fact that each code-motion decision is made locally and independently.

6. Advanced Code Motion Techniques

If our target machine is statically scheduled and has plenty of instruction-level parallelism, we may need a more aggressive algorithm. Here is a high-level description of further extensions:

1.                 To facilitate the extensions below, we can add new basic blocks along control-flow edges originating from blocks with more than one predecessor. These basic blocks will be eliminated at the end of code scheduling if they are empty. A useful heuristic is to move instructions out of a basic block that is nearly empty, so that the block can be eliminated completely.

2.         In Algorithm 10.11, the code to be executed in each basic block is scheduled once and for all as each block is visited. This simple approach suffices because the algorithm can only move operations up to dominating blocks. To allow motions that require the addition of compensation code, we take a slightly different approach. When we visit block B, we only schedule instructions from B and all its control-equivalent blocks. We first try to place these instructions in predecessor blocks, which have already been visited and for which a partial schedule already exists. We try to find a destination block that would lead to an improvement on a frequently executed path and then place copies of the instruction on other paths to guarantee correctness. If the instructions cannot be moved up, they are scheduled in the current basic block as before.

3.         Implementing downward code motion is harder in an algorithm that visits basic blocks in topological order, since the target blocks have yet to be

scheduled. However, there are relatively fewer opportunities for such code motion anyway. We move all operations that

(a)              can be moved, and

(b)             cannot be executed for free in their native block.

This simple strategy works well if the target machine is rich with many unused hardware resources.

7. Interaction with Dynamic Schedulers

A dynamic scheduler has the advantage that it can create new schedules ac-cording to the run-time conditions, without having to encode all these possible schedules ahead of time. If a target machine has a dynamic scheduler, the static scheduler's primary function is to ensure that instructions with high latency are fetched early so that the dynamic scheduler can issue them as early as possible.

Cache misses are a class of unpredictable events that can make a big differ-ence to the performance of a program. If data-prefetch instructions are avail-able, the static scheduler can help the dynamic scheduler significantly by placing these prefetch instructions early enough that the data will be in the cache by the time they are needed. If prefetch instructions are not available, it is useful for a compiler to estimate which operations are likely to miss and try to issue them early.

If dynamic scheduling is not available on the target machine, the static scheduler must be conservative and separate every data-dependent pair of op-erations by the minimum delay. If dynamic scheduling is available, however, the compiler only needs to place the data-dependent operations in the correct order to ensure program correctness. For best performance, the compiler should as-sign long delays to dependences that are likely to occur and short ones to those that are not likely.

Branch misprediction is an important cause of loss in performance. Because of the long misprediction penalty, instructions on rarely executed paths can still have a significant effect on the total execution time. Higher priority should be given to such instructions to reduce the cost of misprediction.

8. Exercises for Section 10.4

Assume a machine that uses the delay model of Example 10.6 (loads take two clocks, all other instructions take one clock).  Also assume that the machine can execute any two instructions at once.  Find a shortest possible execution of this fragment. Do not forget to consider which register is best used for each of the copy steps. Also, remember to exploit the information given by register descriptors as was described in Section 8.6, to avoid unnecessary loads and stores.