Chapter: Genetics and Molecular Biology: Biological Assembly, Ribosomes and Lambda Phage
Geometry of Capsids
The Geometry of Capsids
Previously, we saw that lambda’s genes are crowded
together and even overlapping in places. Other bacterial virus genomes are
similarly squeezed, and it is likely that survival of many types of viruses
depends on their packing as much information as possible into as short a genome
as possible. This being the case, it is likely that as few genes as possible
will be used to code for DNA encapsidation. What general principles might then
apply to the structure of such viruses?
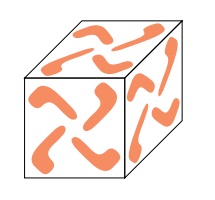
A virus coat could be constructed like a regular
polyhedron. For example, 24 identical subunits could form a cube with one
subunit at
Figure
21.11 A cube withsubunits at each
vertex.
Note that
each of the 24 subunits would make identical contacts with its neighbors. The
maximum vol-ume that could be enclosed by a set of subunits, each making
identical contact with its neighbors, is based on the 20-sided icosahedron
(Fig. 21.12). Each face could consist of three subunits. Thus the maximum
number of subunits that can be utilized to enclose a volume in which each
subunit is exactly equivalent to any other is 60. Experimentally, however, many
viruses, lambda included, are found to be approximately icosahedral but to
possess more than 60 subunits in their coats.
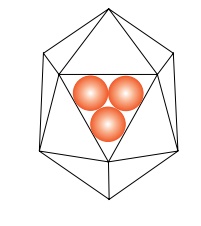
Figure 21.12 A regular icosa-hedron.
Caspar and Klug have investigated the structures
that can be con-structed when the constraint that each subunit be exactly
equivalent to any other is weakened to permit them to be only quasi-equivalent.
That is, each subunit will have nearly the same shape, but will still make
homologous contacts with its neighbors. Using the same contact points over and
over necessitates that the final structure be symmetrical. Maximizing the
similarity of contacts with neighbors necessitates that the structure be helical
or a variation on an icosahedron. We shall consider only those based on
icosahedra.
The restriction to icosahedral symmetry can be most
easily under-stood by considering why some other symmetry is less favored. For
example, why is a large cubic structure unlikely? Suppose a large planar
network of subunits is to be converted to a cube. One of the eight vertices of
a cube can be generated by converting a point of fourfold symmetry to a point
of threefold symmetry by removing a semi-infinite quadrant of subunits (Fig.
21.13). Repeating this process at the other seven vertices generates the cube.
In such a structure there are three kinds of subunit interactions; between
subunits on the same face, between subunits across an edge, and between
subunits at a vertex. When the cube contains 24 subunits, each subunit engages
in each of these three types of interactions and is equivalent to any other
subunit. When the cube possesses more subunits, however, not all subunits
engage in these three types of interactions, and the different subunits are
non-equivalent and therefore distorted with respect to one another.
A similar analysis can be performed if a plane is
covered with equilateral triangles and some points of sixfold symmetry are
converted to points of fivefold symmetry. Of course, if the fivefold symmetric
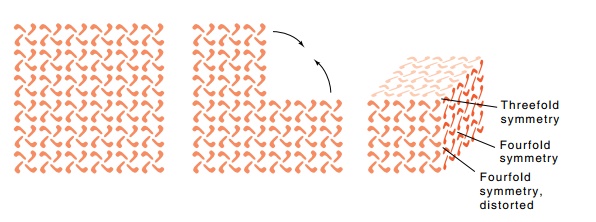
Figure
21.13 Conversion of a planar net of
subunits to a cube by removing asector of the plane and bringing the edges
together.
vertices are adjacent to one another, a regular
icosahedron is generated. If the fivefold vertices are not adjacent, and a
larger volume is enclosed, then again three types of interactions are possible,
but the differences amongst them are smaller, and hence the required distortions
are smaller than in the cubic case. Hence, nature frequently will choose to
construct virus coats based on the five and six neighbor structure. Often the
units possessing the fivefold or sixfold symmetry can be isolated intact or
observed as a unit in the electron microscope. These cap-someric polymers are
called pentons and hexons.
One way to view some, but not all, of the
higher-order structures is that they subdivide the equilateral triangles of the
regular icosahedron. The triangles can be subdivided into 4, 9, 16, 25, and so
on, subtriangles. Other icosahedra, however, are also possible. Consider a
plane net of equilateral triangles and unit vectors a and b (Fig. 21.14).
Satisfactory icosahedra can be constructed if one of the fivefold vertices is
placed at an origin and the second at position (na, mb), where n and m
are integers. If we define T = (n2 + nm + m2), then the regular icosahedron
has T = 1 since n = 1 and m = 0. The number of subunits, S, in all the
Figure
21.14 Coordinates for locating vertices
of an icosahedron with quasi-equivalent subunits. X is one vertex and Y the
second, which is located 2 units in the a
direction and 1 unit in the b
direction.
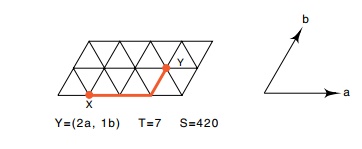
icosahedra is S = 60T. Although the coat of lambda
phage is based on a T = 7 icosahedron, it uses two types of coat protein. The
two bear a fixed spatial relationship to one another as though they derived
from a single
polypeptide chain with a segment removed. In
addition to these proteins, smaller numbers of other proteins are found in the
head. Some of these form the connection between the head and the tail.
Related Topics