Geo stationary and Non Geo-stationary orbits

Geo stationary and Non Geo-stationary orbits:

1. Geo stationary:

A geostationary orbit is one in which a satellite orbits the earth at exactly the same speed as the earth turns and at the same latitude, specifically zero, the latitude of the equator. A satellite orbiting in a geostationary orbit appears to be hovering in the same spot in the sky, and is directly over the same patch of ground at all times.

A geosynchronous orbit is one in which the satellite is synchronized with the earth's rotation, but the orbit is tilted with respect to the plane of the equator. A satellite in a geosynchronous orbit will wander up and down in latitude, although it will stay over the same line of longitude. Although the terms 'geostationary' and 'geosynchronous' are sometimes used interchangeably, they are not the same technically; geostationary orbit is a subset of all possible geosynchronous orbits.

The person most widely credited with developing the concept of geostationary orbits is noted science fiction author Arthur C. Clarke (Islands in the Sky, Childhood's End, Rendezvous with Rama, and the movie 2001: a Space Odyssey). Others had earlier pointed out that bodies traveling a certain distance above the earth on the equatorial plane would remain motionless with respect to the earth's surface. But Clarke published an article in 1945's Wireless World that made the leap from the Germans' rocket research to suggest permanent manmade satellites that could serve as communication relays.

Geostationary objects in orbit must be at a certain distance above the earth; any closer and the orbit would decay, and farther out they would escape the earth's gravity altogether. This distance is 35,786 kilometers (22,236 miles) from the surface.

The first geosynchrous satellite was orbited in 1963, and the first geostationary one the following year. Since the only geostationary orbit is in a plane with the equator at 35,786 kilometers, there is only one circle around the world where these conditions obtain.

This means that geostationary 'real estate' is finite. While satellites are in no danger of bumping in to one another yet, they must be spaced around the circle so that their frequencies do not interfere with the functioning of their nearest neighbors.

Geostationary Satellites:

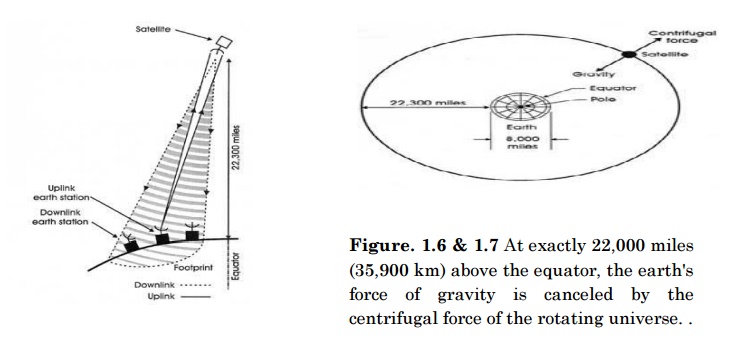
There are 2 kinds of manmade satellites in the heavens above: One kind of satellite ORBITS the earth once or twice a day, and the other kind is called a communications satellite and it is PARKED in a STATIONARY position 22,300 miles (35,900 km) above the equator of the STATIONARY earth.

A type of the orbiting satellite includes the space shuttle and the international space station which keep a low earth orbit (LEO) to avoid the deadly Van Allen radiation belts.

The most prominent satellites in medium earth orbit (MEO) are the satellites which comprise the GLOBAL POSITIONING SYSTEM or GPS as it is called.

The Global Positioning System

The global positioning system was developed by the U.S. military and then opened to civilian use. It is used today to track planes, ships, trains, cars or literally anything that moves. Anyone can buy a receiver and track their exact location by using a GPS receiver.

These satellites are traveling around the earth at speeds of about 7,000 mph (11,200 kph). GPS satellites are powered by solar energy. They have backup batteries onboard to keep them running in the event of a solar eclipse, when there's no solar power.

Small rocket boosters on each satellite keep them flying in the correct path. The satellites have a lifetime of about 10 years until all their fuel runs out.

At exactly 22,300 miles above the equator, the force of gravity is cancelled by the centrifugal force of the rotating universe. This is the ideal spot to park a stationary satellite.

2. Non Geo-Stationary Orbit:

For the geo- stationary case, the most important of these are the gravitational fields of the moon and the sun, and the nonspherical shape of the earth.

Other significant forces are solar radiation pressure and reaction of the satellite itself to motor movement within the satellite. As a result, station- keeping maneuvers must be carried out to maintain the satel- lite within set limits of its nominal geostationary position.

An exact geostationary orbit therefore is not attainable in practice, and the orbital parameters vary with time. The two-line orbital elements are published at regular intervals.

The period for a geostationary satellite is 23 h, 56 min, 4 s, or 86,164 s. The reciprocal of this is 1.00273896 rev/day, which is about the value tabulated for most of the satellites in Fig.

Thus these satellites are geo- synchronous, in that they rotate in synchronism with the rotation of the earth. However, they are not geostationary. The term geosynchronous satellite is used in many cases instead of geostationary to describe these near-geostationary satellites.

It should be noted, however, that in gen- eral a geosynchronous satellite does not have to be near-geostationary, and there are a number of geosynchronous satellites that are in highly elliptical orbits with comparatively large inclinations (e.g., the Tundra satellites).

The small inclination makes it difficult to locate the position of the ascending node, and the small eccentricity makes it difficult to locate the position of the perigee.

However, because of the small inclination, the angles w and Ω can be assumed to be in the same plane.The longitude of the subsatellite point (thesatellitelongitude) is the east early rotation from the Greenwich meridian.

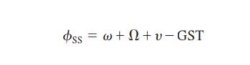
The Greenwich sidereal time (GST) gives the eastward position of the Greenwich meridian relative to the line of Aries, and hence the subsatellite point is at longitudeand the mean longitude of the satellite is given by

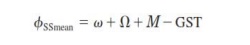
Equation(2.31)can be used to calculate the trueanomaly, and because of the small eccentricity, this can be approximated as v= M + 2esinM.