Gas theory Aeration: Equilibrium, Gas transfer

Gas theory - aeration

How much and how fast gases are transferred in and out of water depends on two factors:

·                 Equilibrium conditions (also known as the sat-uration concentration)

·                 Mass transfer.

Equilibrium is when there is no net transfer of gas in or out of the water. Mass transfer occurs before equilibrium is reached when there is transport of gas into or out of the water.

Equilibrium

When equilibrium has been reached there is no net transport of gas into the water or from the water to the air. There is still some transport of gas mole-cules through the water surface, but what goes in equals what comes out; there are no free gas bubbles in the water. In the same way, when salt is added to freshwater only a certain amount can be dissolved; after reaching this level no more will dis-solve, even if it is added. The excess salt will only remain on the bottom as salt crystals. The same happens with the gas as it stays in bubble form when the water is super-saturated.

To find equilibrium conditions, Henry’s law can be used. Henry’s law can be expressed in several ways;1,9,10 it illustrates that the amount of gas that can be dissolved is proportional to the partial pressure:

Pg=HXg

where:

Pg=partial pressure of gas (atm)

H =Henry’s constant (atm/mol fraction)

Xg=concentration of gas in water (mol gas/(molgas +mol water)).

If SI units are used, Pg is given in pascal (Pa) H in Pa m3/mol and Xg in mol/m3.

Henry’s constant depends on temperature and gas type; its value increases with temperature. The gas obeys Henry’s law if the gas that can be dis-solved in water decreases with temperature.

As explained in section 8.2, partial pressure, Pg, depends on how much of the actual gas is in the atmosphere above the water surface. The pressure it exerts on the surface will press the gas into the water. In air there is about 20% oxygen, so Pgis in this case 0.2; if the atmosphere is pureoxygen, i.e. there is 100% oxygen above the water,Pg=1.0.

If the gas above the water surface is above normal atmospheric pressure, there will be new equilibrium conditions given by Dalton’s law:8

pi=pt y

where:

pi=partial pressure of gas i

pt=total pressure of a mixture of gases

y  =mol fraction of gas i (mol gas i/mol total gases).

Thus if the total pressure of the gas is increased, the partial pressure will also increase and more gas can be pressed into the water.

Henry’s law can be combined with Dalton’s law to give the Henry–Dalton law:

pt y =Hxi

where:

y = mol gas i

pt=total gas pressure H =Henry’s constant

xi=amount of gas i in the liquid.

xiis the key value because, as the equation shows,by increasing the total pressure or by increasing the amount of gas i in the atmosphere, the gas concen-trations in the liquid will be increased.

For instance, when air is under pressure above the water surface, more gas will be pressed into the water which will be super-saturated.

Super-saturation with nitrogen from the air is harmful to fish, so overpressure of air is unwanted and must be avoided. The same may occur if adding air to deep water where the water pressure is higher and the air pressure must be higher than at the surface, i.e. more than 1 atm. To illustrate this, air can be added to the water 2 m deep, but when doing this air is compressed by the water before it dissolves.

Example

A plastic bag containing both air and water is lowered to the bottom of a 2 m deep basin full of water. The air will be compressed by the water pres-sure and the air inside the plastic bag will be pressed into the water because the pressure on the water surface increases. We can now see what will happen to the nitrogen saturation. The normal pressure on the surface is 1 atm (10 mH2O); when lowering the bag to 2 m deep the total pressure will increase to 12 mH2O. The Henry–Dalton law can be used to find the concentration of nitrogen:

pt y =Hx

y is constant, but the pressure increases from 10 to 12 mH2O, a 20% increase. Since H is a constant, x will increase by 20%. Therefore the concentration of nitrogen increases by 20% which is harmful to fish. Under practical conditions, however, some nitrogen will go directly to the surface and escape without having time for gas transfer, but an increase in con-centration of 0.5% per 10 cm or 5% per metre depth occurs.

Adding air directly into the water at depths of more than 1 m is not recommended because super-saturation of nitrogen should be avoided.

Gas transfer

To describe the mechanism of gas transfer into water, the two-film theory proposed by Lewis and Whitman in 1924 is the simplest and most com-monly used (Fig. 8.1; refs 11–13). The interface between the water and the gas can be divided into two films with laminar flow, one gas film and one liquid film. These films will inhibit the transport of gas molecules either into the water or out of the water. The thickness of the two films with laminar flow depends on the amount of turbulence in the

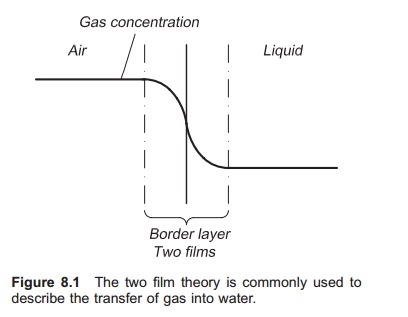
water and in the air; much turbulence results in reduced thickness. To achieve a good transport of gas molecules it is important to have a thin film to increase the velocity of the gas transfer through the interface.

When gas molecules from the air are pressed into the water, they at first go from the gas phase into the gas film, also referred to as the surface film. This process is a combination of diffusion and convec-tion, and is quite fast. The next step is through the gas–liquid film interface where the force is diffu-sion. Diffusion, which results from random molec-ular movements, is a slow process and this step is rate limiting. The last step is transfer of gas into the liquid; the main force here is convection.

The gas transfer per unit time through the surface can be described by the following differen-tial equation:

dc/dt=KL(A/V)(C* −C0)

where:

dc/dt= change in concentration per unit time (mg/(l h))

KL  = coefficient for gas transfer (cm/h)

A/V =contact area of the gas–liquid interface (cm2)in relation to the total liquid volume (cm3)

C*=saturation concentration for the gas in theliquid (mg/l)

C0=starting concentration of the gas in theliquid (mg/l).

The diffusion constant KL is proportional to the dif-fusion rate through the surface film and inversely

proportional to the surface film thickness. This shows the importance of a thin surface film. KL is also dependent on temperature; it will increase with temperature, because the diffusion velocity will increase. The following relationship shows this:

KL= K20qT−20

where:

KL=overall mass transfer coefficient

K20=transfer coefficient at 20°C

q  = correction factor (1.024 for freshwater)

T = temperature.

It is normal to express the constant KL and the contact area (A/V) together as the KLA value, which is known as the overall mass transfer coefficient for an aeration system. It is difficult to calculate KLA for an aeration system; however, if this value could be found it would be easy to calculate the efficiency of the aeration system. Mathematical models have been developed, but they are difficult to use. There-fore the KLA value for an aeration system is usually determined by experiment.

The gas concentration in a system after time t with mass transfer for a given KLA value can be found by integration of the basic equation to give the following result:

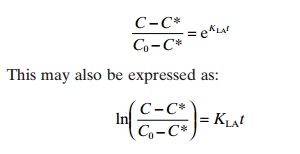
This shows that the concentration (C) after using an aeration system for time t depends on the start-ing concentration (C0), the saturation concentration (C*) and the KLAvalue:

C = C*+(C0− C*)eKLAt

When all the oxygen has been removed from the water and aeration is started, the content of oxygen will increase rapidly and later level off at the limitation value (100% or full saturation); see Fig. 8.2. The value (C−C*)/(C0− C*) is known as the oxygen deficit. If the natural logarithm (ln) of the oxygen deficit is plotted on the y-axis in a diagram with time on the x-axis, the KLA value will be given by the slope of the line.