Chapter: Civil : Railway Airport Harbour Engineering : Railway Engineering : Track and Track Stresses
Forces Acting on the Railway Track
Forces Acting on
the Track
A rail is
subjected to heavy stresses due to the following types of forces.
(a) Vertical
loads consisting of dead loads, dynamic augment of loads including the effect
of speed, the hammer blow effect, the inertia of reciprocating masses, etc.
(b) Lateral
forces due to the movement of live loads, eccentric vertical loading, shunting
of locomotives, etc.
(c)
Longitudinal forces due to tractive
effort and braking forces, thermal forces, etc.
(d)
Contact stresses due to wheel and rail
contact.
(e)
Stresses due to surface defects such as
flat spots on wheels, etc.
1
Vertical Loads
Dead load of
vehicles at rail-wheel contact
The value of dead load is usually taken from the
axle-load diagram. It is, however, brought out that for various reasons the
actual wheel loads, even in the static state on a level and perfect track, may
be different from the nominal values. Cases have sometimes come to notice where
a steam locomotive had a higher axle load than the nominal load or had
different right and left wheel loads.
Dynamic augment
of vertical loads
On
account of vertical impact due to speed and rail vibrations, etc., the dynamic
load is much more than the static load. The dynamic wheel load is obtained by
increasing the static wheel load by an incremental amount given by the speed
factor. Till 1965 Indian Railways used the 'Indian Formula' for calculating the
speed factor. This formula is the following:

where
V is the speed in km/h.
At
a speed of 60 mph, the Indian formula gives a speed factor of 55%, whereas the
German formula, as used by RDSO, gives a speed factor of 30%. Investigations
have been carried out by RDSO and different values of speed factors have been
recommended for different types of vehicles running at different speeds.
Hammer blow
effect
The
centrifugal forces due to revolving masses in the driving and coupled wheels of
a locomotive, such as crank pins, coupling rods, and parts of the connecting
rod, are completely balanced by placing counterweights near the rim of the
wheel, diametrically opposite to the revolving masses. The reciprocating masses
of the piston, piston rod, cross head, and part of the connecting rod, by
virtue of their inertia and oscillatory movement, produce alternating forces in
the direction of the stroke and tend to cause the locomotive to oscillate
sideways and nose across the track. In order to reduce this nosing tendency, a
weight is introduced onto the wheels at the opposite side of the crank. The
horizontal component of the centrifugal force of this added weight balances the
inertial force in the line of stroke, but the vertical component throws the
wheel out of balance in the plane perpendicular to the line of stroke. The
vertical component of the centrifugal force of the weight introduced to balance
the reciprocating masses causes variation in the wheel pressure on the rail,
and is called the hammer blow. The heavier the weight added to balance
the reciprocating masses, the greater the hammer blow.
The
hammer blow effect occurs only in the case of steam locomotives. The hammer
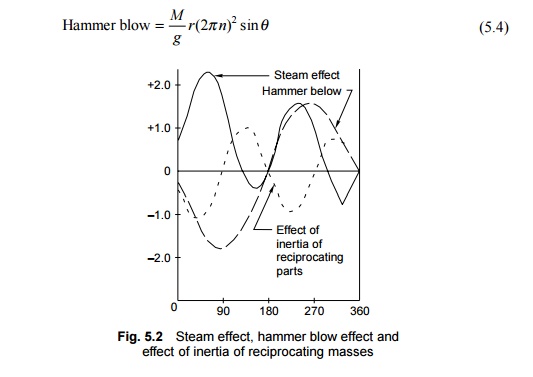
blow can be calculated as follows (Fig. 5.2):
where
M is the net overweight in lbs, r is the crank pin diametre in
ft, n is the number of revolutions of the wheel per second, and ?
is the crank angle.
Steam effect
A
steam locomotive works by converting coal energy into steam energy. Steam
pressure acts on the piston and is transmitted to the driving wheels through
the crank pins and connecting rod. The vertical component of the crank pins and
connecting rod is at an angle to the piston rod. Its value is given by the
formula
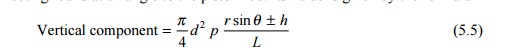
where
L is the length of the connecting rod in inches, h is the height
of the cross head above the centre line of the driving wheel in inches, and ?
is the crank angle, i.e., the angle traversed by the crank since the beginning
of the stroke.
The steam effect (Fig. 5.2) does not scynchronize
with the hammer blow effect due to overbalance and is additional to the hammer
blow only during some part of the revolution of the crank shaft.
Inertia of
reciprocating masses
The
reciprocating masses, due to their inertia and acceleration, alter the forces
on the piston, and hence the force in the connecting rod is also affected
during the revolution of the wheel.
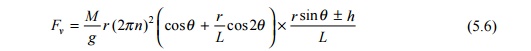
where
M is the mass of the reciprocating parts, L is the length of the
connecting rod, n is the number of revolutions per second, h is
the height of the cross head above the centre line of the driving wheel, and ?
is the crank angle.
The maximum combined force of the hammer blow, the
steam effect, and inertia for each driving wheel and the hammer blow effect of
the coupled wheels do not act simultaneously due to the phase difference in the
angular position of the counterweights in the coupled and driving wheels. The
maximum combined effect of these forces is obtained by summing up the three curves
for one complete revolution of the wheel.
Bending stresses
on the rail due to vertical loads
The
general theory of bending of rails is based on the assumption that the rail is
a long bar continuously supported by an elastic foundation. Due to vertical
loads, the rail is subjected to bending or flexural stresses. The bending
stresses that a rail is subjected to as a result of vertical loads are
illustrated in Fig. 5.3. The theory of stresses in rails takes into account the
elastic nature of the supports. Based on this theory, the formula for bending
moment is
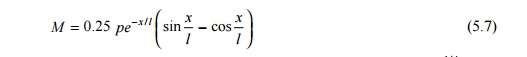
where M is the bending moment, P is the
isolated vertical load, l ? (EI/?)1/ 4 is
the characteristic length, EI is the flexural stiffness of the rail, ?
is the track modulus, and x is the distance of the point from the load.

According
to Eqn (5.7), the bending moment is zero at points where x ? ? l /4,
3? l/4 and maximum where x ? 0 , ? l /2, 3?
l/2 , etc.
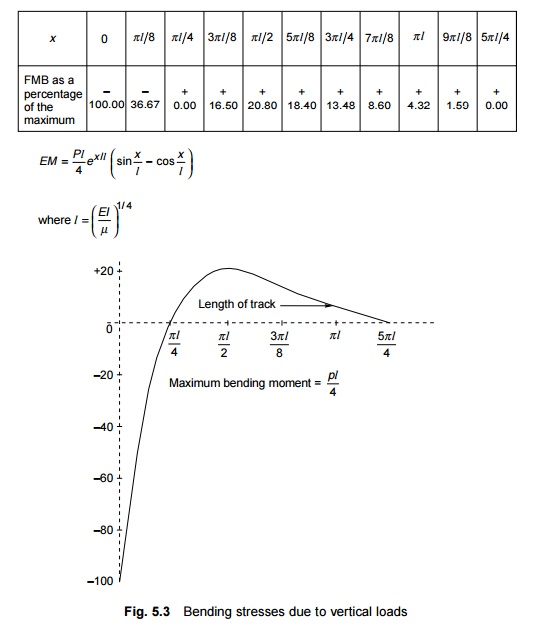
For calculating the stresses acting on the rail,
first the maximum bending moment caused due to a series of loads moving on the
rail is calculated as per Eqn (5.7). The bending stress is then calculated by
dividing the bending moment by the sectional modulus of the rail. The
permissible value of bending stress due to a vertical load and its eccentricity
is 23.5 kg/mm2 for rails with a 72 UTS.
2
Stresses on the Track
Stresses
on the track due to the various kinds of forces applied on it are discussed in
the following sections.
Lateral forces
The
lateral force applied to the rail head produces a lateral deflection and twist
in the rail. Lateral force causes the rail to bend horizontally and the
resultant torque causes a huge twist in the rail as well as the bending of the
head and foot of the rail. Lateral deflection of the rail is resisted by the
friction between the rail and the sleeper, the resistance offered by the rubber
pad and fastenings, as well as the ballast coming in contact with the rail.
The combined effect of lateral forces resulting in
the bending and twisting of a rail can be measured by strain gauges. Field
trials indicate that the loading wheels of a locomotive may exert a lateral
force of up to 2 t on a straight track particularly at high speeds.
Longitudinal
forces
Due
to the tractive effort of the locomotive and its braking force, longitudinal
stresses are developed in the rail. Temperature variations, particularly in
welded rails, result in thermal forces, which also lead to the development of
stresses. The exact magnitude of longitudinal forces depends on many variable
factors. However, a rough idea of these values is as follows:
(a) Longitudinal
forces on account of 30-40% weight of locomotive of tractive effort for
alternating current (ac).
(b)
Longitudinal forces on account of 15-20%
of weight of braking force of the
locomotive
and 10-15% weight of trailing load.
Tensile stresses are induced in winter due to
contraction and compressive stresses are developed in summer due to
compression. The extreme value of these stresses can be 10.75 kg/mm2
in winter and 9.5 kg/mm2 in summer.
Contact stresses
between rail and wheel
Hertz
formulated a theory to determine the area of contact and the pressure
distribution at the surface of contact between the rail and the wheel. As per
this theory, the rail and wheel contact is similar to that of two cylinders
(the circular wheel and the curved head of the rail) with their axes at right
angles to each other. The area of contact between the two surfaces is bound by
an ellipse as shown in Fig. 5.4.
The
maximum contact shear stress (F) at the contact point between the wheel
and the rail is given by the empirical formula

where
F is the maximum shear stress in kg/mm2, R is the
radius of the fully worn out wheel in mm, and P is the static wheel load
in kg + 1000 kg for on-loading on curves
Contact
stress for the WDM2 locomotive Static wheel load (P)
= 9400 + 1000 = 10,400 kg. Radius of worn out wheel for maximum wear of 76
mm (38 mm radius reduction):
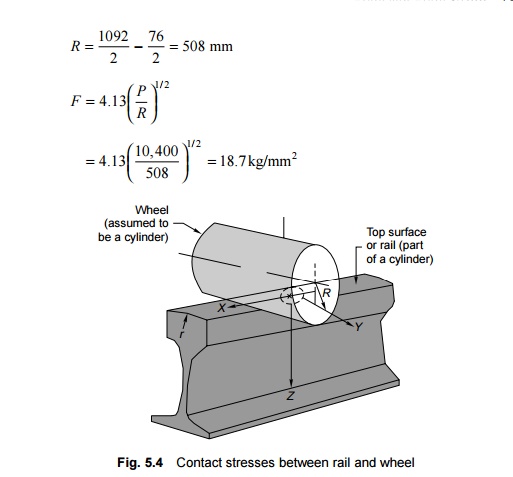
The
contact stress for the WDM2 locomotive as such is 18.7 kg/mm2. The
maximum value is, however, limited to 21.6 kg/mm2, which is 30% of
the UTS value (72 kg/mm2) of the rail.
Surface defects
A
flat on the wheel or a low spot on the rail causes extra stresses on the rail
section. Empirical studies reveal that an additional deflection of about 1.5
times the depth of the flat or low spot occurs at the critical speed (about 30
km/h). Additional bending moment is caused on this account with a value of
about 370,000 kg cm for the BG group A route with the WDM4 locomotive.
Stresses on a
sleeper
The
sleepers are subjected to a large number of forces such as dead and live loads,
dynamic components of tracks such as rails and sleeper fastenings, maintenance
standards, and other such allied factors. Based on the elastic theory, the
maximum load on a rail seat is given by the following formula:
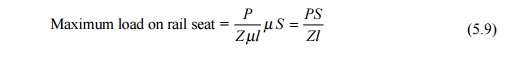
where
P is the wheel load, µ is the track modulus, S is the
sleeper spacing, l is the characteristic length, and Z is the
modulus of the rail section.
The maximum load on the
rail seat is 30%-50% of the dynamic wheel load, depending on various factors
and particularly the packing under the sleeper.
The distribution of load under the sleeper is not
easy to determine. The pattern of distribution depends on the sleeper as well
as on the firmness of the packing under the sleeper. As the ballast yields
under the load, the pressure under the sleeper is not uniform and varies
depending on the standard of maintenance. The following two extreme conditions
may arise.
End-bound
sleeper The newly compacted ballast is well compacted under
the sleeper and the ends of the sleepers are somewhat hard packed. The
deflection of the sleeper at the centre is more than that at the ends.
Centre-bound
sleeper As trains pass on the track, the packing under the
sleeper tends to become loose because of the hammering action of the
moving loads. The sleeper thus tends to be loose under the rail seat.
Alternatively, due to defective packing, the sleeper is sometimes hard packed
at the centre.
Stresses on
ballast
The
load passed onto the sleeper from the rail is in turn transferred to the
ballast. The efficacy of this load transmission depends not only on the
elasticity of the sleeper but also on the size, shape, and depth of the ballast
as well as the degree of compaction under the sleeper. Professor A.N. Talbot
has analysed the pressure distribution in the ballast under the sleeper and
investigations reveal that the pressure distribution curve under the sleeper
would be shaped like bulbs as shown in Fig. 5.5.
The
following are the important conclusions drawn from Fig. 5.5.
(a)
The pressure on the sleeper is maximum
at the centre of its width. This pressure decreases from the centre towards the
ends.
(b)
The vertical pressure under the sleeper
is uniform at a depth approximately equal to the spacing between the sleepers.
Pressure on
formation or subgrade
The
live as well as dead loads exerted by the trains and the superstructure are
finally carried by the subgrade. The pressure on the subgrade depends not only
on the total quantum of the load but also on the manner in which it is
transferred to the subgrade. The spacing between the sleepers; the size, depth,
as well as compaction of the ballast under the sleeper; and the type of
subgrade play an important role in the distribution of pressure on the
subgrade.
The values of maximum formation pressure permitted
on Indian Railways are the following:
For
motive power

For
goods wagons

Relief of
stresses
A
train load consists of a number of wheel loads close to each other which act
simultaneously on the rail. A single isolated wheel load creates much more
bending moment in the rail as compared to a group of wheel loads, which on
account of the negative bending moment under adjacent wheels provide what known
as a 'relief of stresses'. The rail stresses in this case are comparatively
smaller. The value of relief of stresses depends upon the distance of the point
of contraflexure of the rail and the spacing between the wheels, but its value
can be as high as 50%.
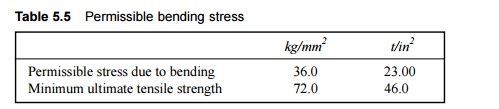
Permissible
stresses on a rail section
The
permissible bending stresses due to vertical load and its eccentricity, and
lateral load on a rail section on Indian Railways is given in Table 5.5.
Table
5.5 Permissible
bending stress
The
stresses on a rail are measured by any of the following methods depending upon
the facilities available.
(a)
Photo-elastic method
(b)
Electric resistance strain gauge method
(c)
Method employed using special test frame
At present, Indian Railways mostly uses the electric
resistance strain gauges for measuring rail stresses.
Whenever
a new locomotive or rolling stock design is introduced on the Railways, a
detailed study is carried out followed by field trials to ensure that the
permitted speed of the new locomotive or rolling stock does not cause excessive
stresses on the track. The same stipulations are made whenever there is an
increase in the speed or axle load of the existing locomotive or rolling stock
design.
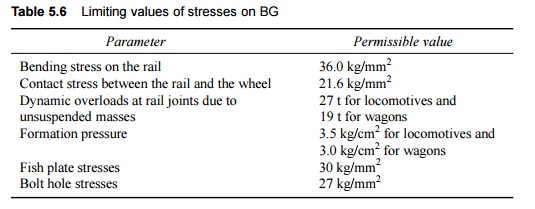
The various parameters and their limiting values
required to be checked for BG are given in Table 5.6.
Table
5.6 Limiting values
of stresses on BG
Related Topics