Entropy

 ENTROPY

The first law of thermodynamics deals with the property energy and the conservation of energy. The second law introduced in the previous chapter, leads to the definition of a new property called entropy. Entropy is defined in terms of a calculus operation, and no direct physical picture of it can be given. In this chapter, Clausius inequality, which forms the basis for the definition of entropy will be discussed first. It will be followed by the discussion of entropy changes that take place during various processes for different working fluids. Finally, the reversible steady-flow work and the isentropic efficiencies of various engineering devices such as turbine and compressors will be discussed.

The Clausius Inequality

Consider two heat engines operating between two reservoirs kept at temperature T_H and T_L as shown in the Figure 5.1. Of the two heat engines, one is reversible and the other is irreversible.

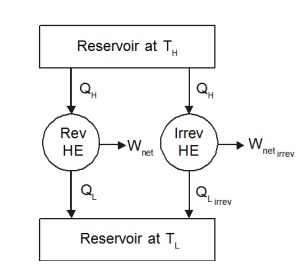
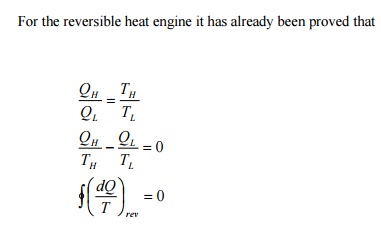
As discussed earlier, the work output from the irreversible engine should be less than that of the reversible engine for the same heat input Q_H. Therefore Q_L,Irrev will be greater than Q_L,Rev . Let us define

QL,Irrev =QL,Rev +dQ

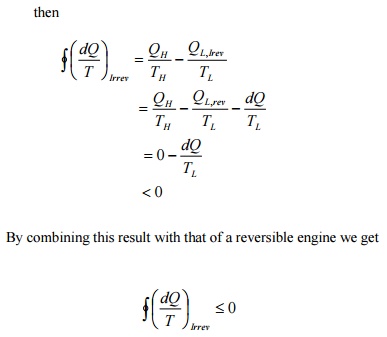
This is known as Clausius inequality.

Clausius inequality forms the basis for the definition of a new property known as entropy.

Consider a system taken from state 1 to state 2 along a reversible path A as shown in Figure 5.2. Let the system be brought back to the initial state 1 from state 2 along a reversible path B. Now the system has completed one cycle. Applying Clausius inequality we get

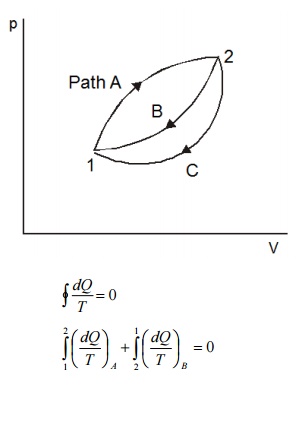
Instead of taking the system from state2 to state1 along B, consider another reversible path C. Then for this cycle 1-A-2-C-1, applying Clausius inequality :

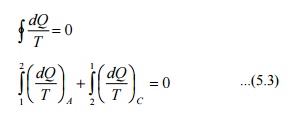
Comparing 5.2 & 5.3

Hence, it can be concluded that the quantity is a point function, independent of the path followed. Therefore it is a property of the system. Using the symbol S for entropy we can write

upon integration we get

For a reversible process.

Entropy change for an irreversible process

The relationship between the entropy change and heat transfer across the boundary during an irreversible processes can be illustrated with a simple cycle composed of two processes, one of which is internally reversible and the other is irreversible, as shown in Figure 5.3. The Clausius inequality applied to this irreversible cycle can be written as

Since the process B is internally reversible, this process can be reversed, and therefore

As defined in equation 5.5, since the process B being reversible the integral on the left hand side can be expressed as

Temperature - Entropy diagram

In a T-s diagram consider a strip of thickness ds with mean height T as shown in Figure 5.4. Then Tds gives the area of the strip.

For a reversible process the elemental heat transfer

dQ =Tds =Area of the strip

To get the total heat transfer the above equation should be integrated between the limits 1 and 2, so that, we get

This is equivalent to the area under a curve representing the process in a T-S diagram as shown in the Fig 5.4.

Note:  ^–For an isothermal process S₂ -S₁ =.

    ^–For reversible adiabatic process S₂ -S₁ =0.

Change in Entropy

a)  Solids and Liquids

Change in entropy

Where  dq  =du + pdv

For solids and liquids

pdv =  0

Where c- is the specific heat

b)      For ideal gases change in entropy

Substituting

du  =C_v dT

  We get ,Upon integration

Substituting dh  =C_p dT

and We get

Upon integration

Principle of Increase in Entropy

Applying Clausius inequality,

For an isolated system undergoing a process

Consider a system interacting with its surroundings. Let the system and its surroundings are included in a boundary forming an isolated system. Since all the reactions are taking place within the combined system, we can express

or

Whenever a process occurs entropy of the universe (System plus surroundings) will increase if it is irreversible and remain constant if it is reversible. Since all the processes in practice are irreversible, entropy of universe always increases

ie.,     (Ds)_universe>0

This is known as principle of increase of entropy.

Adiabatic Efficiency of Compressors and Turbines

In steady flow compressors and turbines reversible adiabatic process is assumed to be the ideal process. But due to the irreversibilities caused by friction between the flowing fluid and impellers, the process is not reversible though it is adiabatic. Percentage deviation of this process from the ideal process is expressed in terms of adiabatic efficiency.

(a) Compressors :

Since compressors are work consuming devices actual work required is more than ideal work. For compressors handling ideal gases

(b) Turbines :

In turbine due to irreversibilities the actual work output is less than the isentropic work.

Solved Problems

Prob : 5.1             A body at 200oC undergoes an reversible isothermal process. The heat energy removed in the process is 7875 J. Determine the change in the entropy of the body.

Comment :  Entropy decreases as heat is removed from the system.

Prob : 5.2             A mass of 5 kg of liquid water is cooled from 100oC to 20oC. Determine the change in entropy.        

System                 :         Closed system     

Comment            :  Entropy decreases as heat is removed from the system.

Prob : 5.3 Air is compressed isothermally from 100 kPa to 800 kPa. Determine the change in specific entropy of the air.

System  :  Closed/Open

Known  :  p₁  =100 kPa

p₂  =800 kPa

To find :  DS - change in Specific entropy

Analysis    :   DS   = -R ln  [Since the process is isothermal]

= 0 .287- x ln

 =  0.597 -kJ/kgK.

Prob : 5.4 A mass of 5 kg of air is compressed from 90 kPa, 32^oC to 600 kPa in a polytropic process, pV^1.3=constant. Determine the change entropy.

System  :  Closed / Open

Known  :  p₁  =90 kPa

T₁ =32^oC =305 K

p₂  =600 kPa

m  =5  kg

Process :  pV^1.3 =Constant

To find :  DS - Change in entropy

Analysis      :    S₂  -S₁  =m

Where T₂  =T₁

 =305

=473 K

\ S₂  -S₁  =5  

=-0.517 kJ/K.

Comment  :   For air the ratio of Cp and Cv is equal to 1.4. Therefore the polytropic index  n -1.3(<1.4) indicates that some heat is removed from the system resulting in negative entropy.

Prob : 5.5 A rigid insulated container holds 5 kg of an ideal gas. The gas is stirred so that its state changes from 5 kPa and 300 K to 15 kPa. Assuming C_p =1.0 kJ/kgK and g =1.4, determine the change of entropy of the system.

System  :  Closed

Process :  Constant volume since the gas is stirred in an rigid container

 3 .922  kJ/K    =

Comment : Though this process is adiabatic it is not isentropic since the process of stirring is an irreversible process.

Prob : 5.6 An insulated rigid vessel is divided into two chambers of equal volumes. One chamber contains air at 500 K and 2 MPa. The other chamber is evacuated. If the two chambers are connected d, what would be the entropy change ?

System  :  Closed system

Process :  Unresisted expansion

=0.199 kJ/kgK

Comment  :   Though the process is adiabatic entropy increases as the process involving

unresisted expansion is an irreversible process. It also proves the fact

Prob : 5.7 An adiabatic chamber is partitioned into two equal compartments. On one side there is oxygen at 860 kPa and 14^oC. On the other side also, there is oxygen, but at 100 kPa and 14^oC. The chamber is insulated and has a volume of 7500 cc. The partition is abruptly removed. Determine the final pressure and the change in entropy of the universe.

Prob : 5.8 A closed system is taken through a cycle consisting of four reversible processes. Details of the processes are listed below. Determine the power developed if the system is executing 100 cycles per minutes.