Chapter: Mechanical : Engineering Thermodynamics : The Second Law of Thermodynamics
Available Energy, Availability And Irreversibility
AVAILABLE ENERGY, AVAILABILITY AND
IRREVERSIBILITY
From second law of thermodynamics we found that
complete conversion of heat into work is not possible in a continuous process.
Also it has been proved that the most efficient cycle to produce work is a
reversible power cycle (Carnot cycle). Even in carnot cycle, the efficiency of
conversion can never be
unity and hence to
establish a comparison of the work-energy conversion in actual processes, the
maximum theoretical work obtainable with respect to some datum must be
determined. This chapter is dedicated for this objective.
Available and Unavailable Energy
The
energy content of a system can be divided into two parts
· Available energy, which under ideal
conditions may be completely converted into work
· Unavailable energy which is usually rejected
as waste.
Consider Q units of heat energy available at a
temperature T. Available part of energy can be obtained by assuming that the
heat is supplied to a Carnot engine. Work obtained from the carnot engine
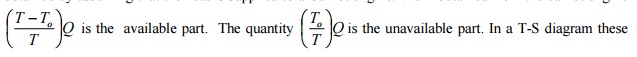
quantities can be
represented as shown in the fig 6.1. The term T0 is the ambient
temperature. Hence it can be concluded that the available and unavailable part
of energy content of a system depends on the ambient conditions also.
Reversible Work In A Non-flow Process
From first law of thermodynamics
Qsys -W=U2-U1 ...6.1
From second law of thermodynamics for a reversible
process

This is also the maximum work in the process.
For a closed system, when undergoing change in
volume, the work done against the atmospheric pressure:
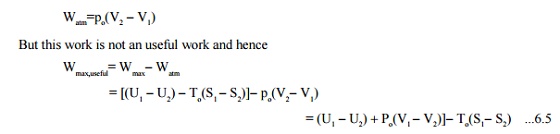
Reversible Work In A Steady-state Control
Volume
Steady flow energy equation for a constant volume is
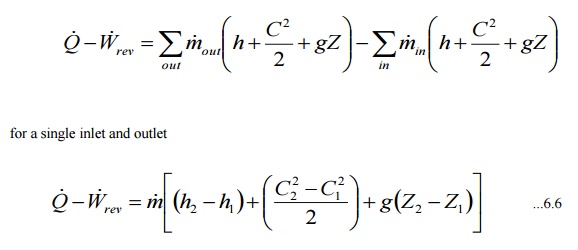

From eqn 6.6 neglecting kinetic and potential energy
changes
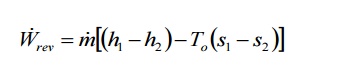
In an open system a
fixed volume in space known as control volume is taken for analysis. Hence the
atmospheric work term po(V1-V2) should not be
considered. Therefore
Wrev= Wmax,useful for an open
system
Availability
The maximum
useful work that can be obtained from the system such that the system comes to
a dead state, while exchanging heat only with the surroundings, is known as
availability of the system. Here the term dead state means a state where the
system is in thermal and mechanical equilibrium with the surroundings.
Therefore for a closed system availability can be
expressed as
f=(U -Uo
)+po (V -Vo
)-To (S-So
)
similarly
for an open system
y=(H -Ho )-To
(S-So )
In steady flow systems
the exit conditions are assumed to be in equilibrium with the surroundings. The
change in availability of a system when it moves from one state to another can
be given as:
for a closed system
f1-f2 =(U1 -U 2 )+po
(V1 -V2 )-To (S1 -S2 ) ...6.10
for an open system
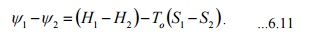
Availability Change Involving Heat Exchange
with Reservoirs
Consider a system undergoing a change of state while
interacting with a reservoir kept at TR and atmosphere at pressure po
and temperature To. Net heat transfer to the system

Qnet= QR-QO.
From first law of thermodynamics
Qnet- Wrev=U2-U1 ...6.12
From second law of thermodynamics, assuming the
process to be reversible
(Ds)Res+(Ds)atm+(Ds)sys=0

The
negative sign for QR shows that the heat is removed from the
reservoir.
By
rearranging We get
Net heat transferred

Irreversibility
Work obtained in
an irreversible process will always be less than that of a reversible process.
This difference is termed as irreversibility (i.e) the difference between the
reversible work and the actual work for a given change of state of a system is
called irreversibility.
I=W -W
rev act
Let a stationary closed
system receiving Q kJ of heat is giving out Wact kJ of work. From
first law of thermodynamics.
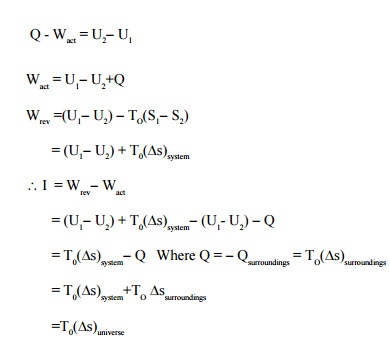
Since (Ds)universe
will be positive for an irreversible flow, irreversibility will be zero for a
reversible process and will never be negative
I ³0 .
Similarly for a steady flow system

Related Topics