Divide and Conquer

Divide-and-Conquer

Whatever man prays for, he prays for a miracle. Every prayer reduces itself to this—Great God, grant that twice two be not four.

—Ivan Turgenev (1818–1883), Russian novelist and short-story writer

Divide-and-conquer is probably the best-known general algorithm design technique. Though its fame may have something to do with its catchy name, it is well deserved: quite a few very efficient algorithms are specific implementations of this general strategy. Divide-and-conquer algorithms work according to the following general plan:

            A problem is divided into several subproblems of the same type, ideally of about equal size.

            The subproblems are solved (typically recursively, though sometimes a dif-ferent algorithm is employed, especially when subproblems become small enough).

            If necessary, the solutions to the subproblems are combined to get a solution to the original problem.

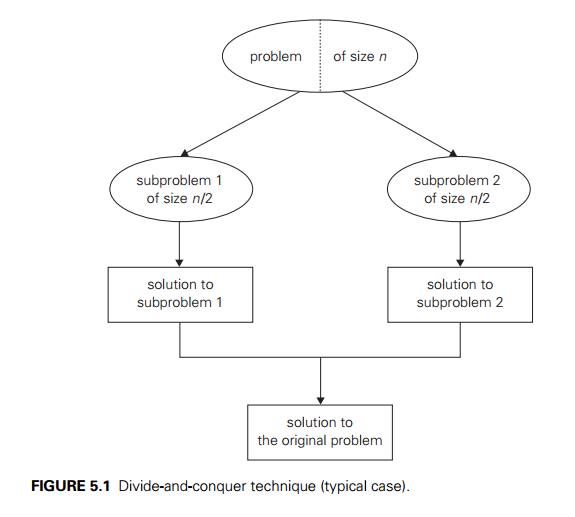
The divide-and-conquer technique is diagrammed in Figure 5.1, which depicts the case of dividing a problem into two smaller subproblems, by far the most widely occurring case (at least for divide-and-conquer algorithms designed to be executed on a single-processor computer).

As an example, let us consider the problem of computing the sum of n numbers a₀, . . . , a_n−1. If n > 1, we can divide the problem into two instances of the same problem: to compute the sum of the first n/2 numbers and to compute the sum of the remaining n/2 numbers. (Of course, if n = 1, we simply return a₀ as the answer.) Once each of these two sums is computed by applying the same method recursively, we can add their values to get the sum in question:

a₀ + ^{. . .} + a_n−1 = (a₀ + ^{. . .} + a _{n/2 −1}) + (a _n/2  + ^{. . .} + a_n−1).

Is this an efficient way to compute the sum of n numbers? A moment of reflection (why could it be more efficient than the brute-force summation?), a

small example of summing, say, four numbers by this algorithm, a formal analysis (which follows), and common sense (we do not normally compute sums this way, do we?) all lead to a negative answer to this question.¹

Thus, not every divide-and-conquer algorithm is necessarily more efficient than even a brute-force solution. But often our prayers to the Goddess of Algorithmics—see the chapter’s epigraph—are answered, and the time spent on executing the divide-and-conquer plan turns out to be significantly smaller than solving a problem by a different method. In fact, the divide-and-conquer approach yields some of the most important and efficient algorithms in computer science. We discuss a few classic examples of such algorithms in this chapter. Though we consider only sequential algorithms here, it is worth keeping in mind that the divide-and-conquer technique is ideally suited for parallel computations, in which each subproblem can be solved simultaneously by its own processor.

As mentioned above, in the most typical case of divide-and-conquer a prob-lem’s instance of size n is divided into two instances of size n/2. More generally, an instance of size n can be divided into b instances of size n/b, with a of them needing to be solved. (Here, a and b are constants; a ≥ 1 and b > 1.) Assuming that size n is a power of b to simplify our analysis, we get the following recurrence for the running time T (n):

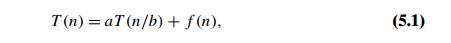
where f (n) is a function that accounts for the time spent on dividing an instance of size n into instances of size n/b and combining their solutions. (For the sum example above, a = b = 2 and f (n) = 1.) Recurrence (5.1) is called the general divide-and-conquer recurrence. Obviously, the order of growth of its solution T (n) depends on the values of the constants a and b and the order of growth of the function f (n). The efficiency analysis of many divide-and-conquer algorithms is greatly simplified by the following theorem (see Appendix B).

For example, the recurrence for the number of additions A(n) made by the divide-and-conquer sum-computation algorithm (see above) on inputs of size n = 2^k is

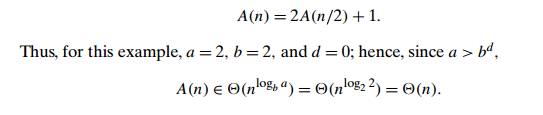
Note that we were able to find the solution’s efficiency class without going through the drudgery of solving the recurrence. But, of course, this approach can only es-tablish a solution’s order of growth to within an unknown multiplicative constant, whereas solving a recurrence equation with a specific initial condition yields an exact answer (at least for n’s that are powers of b).

It is also worth pointing out that if a = 1, recurrence (5.1) covers decrease-by-a-constant-factor algorithms discussed in the previous chapter. In fact, some people consider such algorithms as binary search degenerate cases of divide-and-conquer, where just one of two subproblems of half the size needs to be solved. It is better not to do this and consider decrease-by-a-constant-factor and divide-and-conquer as different design paradigms.