Mergesort

Mergesort

Mergesort is a perfect example of a successful application of the divide-and-conquer technique. It sorts a given array A[0..n − 1] by dividing it into two halves A[0.. n/2 − 1] and A[ n/2 ..n − 1], sorting each of them recursively, and then merging the two smaller sorted arrays into a single sorted one.

ALGORITHM                 Mergesort(A[0..n − 1])

//Sorts array A[0..n − 1] by recursive mergesort //Input: An array A[0..n − 1] of orderable elements

//Output: Array A[0..n − 1] sorted in nondecreasing order

if n > 1

copy A[0.. n/2 − 1] to B[0.. n/2 − 1] copy A[ n/2 ..n − 1] to C[0.. n/2 − 1]

Mergesort(B[0.. n/2                          − 1])

Mergesort(C[0.. n/2                          − 1])

Merge(B, C, A)                            //see below

The merging of two sorted arrays can be done as follows. Two pointers (array indices) are initialized to point to the first elements of the arrays being merged. The elements pointed to are compared, and the smaller of them is added to a new array being constructed; after that, the index of the smaller element is incremented to point to its immediate successor in the array it was copied from. This operation is repeated until one of the two given arrays is exhausted, and then the remaining elements of the other array are copied to the end of the new array.

ALGORITHM                 Merge(B[0..p − 1], C[0..q − 1], A[0..p + q − 1])

//Merges two sorted arrays into one sorted array //Input: Arrays B[0..p − 1] and C[0..q − 1] both sorted

//Output: Sorted array A[0..p + q − 1] of the elements of B and C i ← 0; j ← 0; k ← 0

while i < p and j < q do if B[i] ≤ C[j ]

A[k] ← B[i]; i ← i + 1 else A[k] ← C[j ]; j ← j + 1 k ← k + 1

if i = p

copy C[j..q − 1] to A[k..p + q − 1] else copy B[i..p − 1] to A[k..p + q − 1]

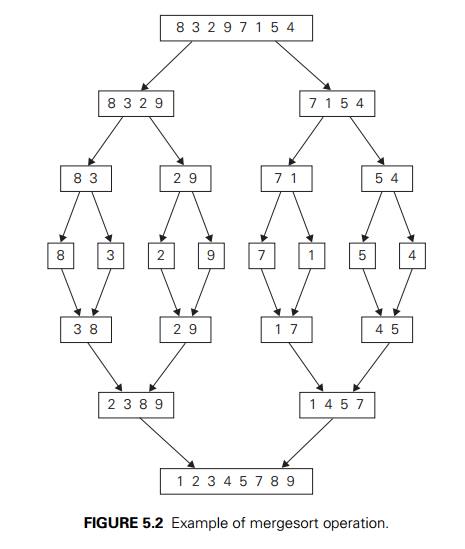
The operation of the algorithm on the list 8, 3, 2, 9, 7, 1, 5, 4 is illustrated in Figure 5.2.

How efficient is mergesort? Assuming for simplicity that n is a power of 2, the recurrence relation for the number of key comparisons C(n) is

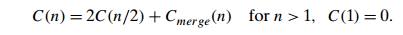
Let us analyze C_merge(n), the number of key comparisons performed during the merging stage. At each step, exactly one comparison is made, after which the total number of elements in the two arrays still needing to be processed is reduced by 1. In the worst case, neither of the two arrays becomes empty before the other one contains just one element (e.g., smaller elements may come from the alternating arrays). Therefore, for the worst case, C_merge(n) = n − 1, and we have the recurrence

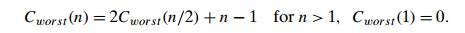
Hence, according to the Master Theorem, C_worst (n) ∈  (n log n) (why?). In fact, it is easy to find the exact solution to the worst-case recurrence for n = 2^k:

C_worst (n) = n log₂ n − n + 1.

The number of key comparisons made by mergesort in the worst case comes very close to the theoretical minimum² that any general comparison-based sorting algorithm can have. For large n, the number of comparisons made by this algo-rithm in the average case turns out to be about 0.25n less (see [Gon91, p. 173]) and hence is also in  (n log n). A noteworthy advantage of mergesort over quick-sort and heapsort—the two important advanced sorting algorithms to be discussed later—is its stability (see Problem 7 in this section’s exercises). The principal short-coming of mergesort is the linear amount of extra storage the algorithm requires. Though merging can be done in-place, the resulting algorithm is quite complicated and of theoretical interest only.

There are two main ideas leading to several variations of mergesort. First, the algorithm can be implemented bottom up by merging pairs of the array’s elements, then merging the sorted pairs, and so on. (If n is not a power of 2, only slight bookkeeping complications arise.) This avoids the time and space overhead of using a stack to handle recursive calls. Second, we can divide a list to be sorted in more than two parts, sort each recursively, and then merge them together. This scheme, which is particularly useful for sorting files residing on secondary memory devices, is called multiway mergesort.

Exercises 5.1

1. a. Write pseudocode for a divide-and-conquer algorithm for finding the po-sition of the largest element in an array of n numbers.

1. b.          What will be your algorithm’s output for arrays with several elements of the largest value?

         c. Set up and solve a recurrence relation for the number of key comparisons made by your algorithm.

         d. How does this algorithm compare with the brute-force algorithm for this problem?

                 2. a. Write pseudocode for a divide-and-conquer algorithm for finding values of both the largest and smallest elements in an array of n numbers.

         b. Set up and solve (for n = 2^k) a recurrence relation for the number of key comparisons made by your algorithm.

         c. How does this algorithm compare with the brute-force algorithm for this problem?

                 3. a. Write pseudocode for a divide-and-conquer algorithm for the exponenti-ation problem of computing aⁿ where n is a positive integer.

         b. Set up and solve a recurrence relation for the number of multiplications made by this algorithm.

         c. How does this algorithm compare with the brute-force algorithm for this problem?

         d. As mentioned in Chapter 2, logarithm bases are irrelevant in most contexts arising in analyzing an algorithm’s efficiency class. Is this true for both asser-tions of the Master Theorem that include logarithms? 

1. Find the order of growth for solutions of the following recurrences.

         T (n) = 4T (n/2) + n, T (1) = 1

         T (n) = 4T (n/2) + n², T (1) = 1

         T (n) = 4T (n/2) + n³, T (1) = 1

         6. Apply mergesort to sort the list E, X, A, M, P, L, E in alphabetical order.

         7. Is mergesort a stable sorting algorithm?

                 8. a. Solve the recurrence relation for the number of key comparisons made by mergesort in the worst case. You may assume that n = 2^k.

         b. Set up a recurrence relation for the number of key comparisons made by mergesort on best-case inputs and solve it for n = 2^k.

         c. Set up a recurrence relation for the number of key moves made by the version of mergesort given in Section 5.1. Does taking the number of key moves into account change the algorithm’s efficiency class?

         9. Let A[0..n − 1] be an array of n real numbers. A pair (A[i], A[j ]) is said to be an inversion if these numbers are out of order, i.e., i < j but A[i] > A[j ]. Design an O(n log n) algorithm for counting the number of inversions.

10.    Implement the bottom-up version of mergesort in the language of your choice.

11. Tromino puzzle A tromino (more accurately, a right tromino) is an L-shaped tile formed by three 1 × 1 squares. The problem is to cover any 2ⁿ × 2ⁿ chess-board with a missing square with trominoes. Trominoes can be oriented in an arbitrary way, but they should cover all the squares of the board except the missing one exactly and with no overlaps. [Gol94]

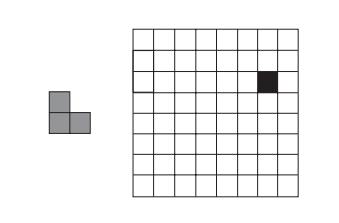
Design a divide-and-conquer algorithm for this problem.