Convex Hull Problems by Divide and Conquer

                The Closest-Pair and Convex-Hull Problems by Divide-and-Conquer

In Section 3.3, we discussed the brute-force approach to solving two classic prob-lems of computational geometry: the closest-pair problem and the convex-hull problem. We saw that the two-dimensional versions of these problems can be solved by brute-force algorithms in  (n2) and O(n3) time, respectively. In this section, we discuss more sophisticated and asymptotically more efficient algorithms for these problems, which are based on the divide-and-conquer technique.

Let us revisit the convex-hull problem, introduced in Section 3.3: find the smallest convex polygon that contains n given points in the plane. We consider here a divide-and-conquer algorithm called quickhull because of its resemblance to quicksort.

Let S be a set of n > 1 points p₁(x₁, y₁), . . . , p_n(x_n, y_n) in the Cartesian plane. We assume that the points are sorted in nondecreasing order of their x coordinates, with ties resolved by increasing order of the y coordinates of the points involved. It is not difficult to prove the geometrically obvious fact that the leftmost point p₁ and the rightmost point p_n are two distinct extreme points of the set’s convex

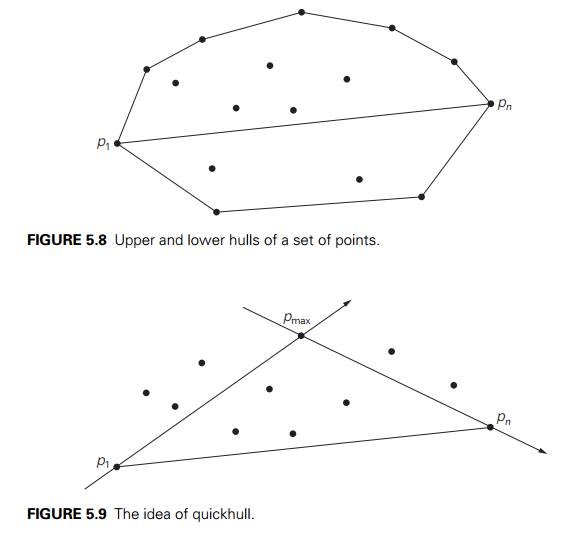
The boundary of the convex hull of S is made up of two polygonal chains: an “upper” boundary and a “lower” boundary. The “upper” boundary, called the upper hull, is a sequence of line segments with vertices at p₁, some of the points in S₁ (if S₁ is not empty) and p_n. The “lower” boundary, called the lower hull, is a sequence of line segments with vertices at p₁, some of the points in S₂ (if S₂ is not empty) and p_n. The fact that the convex hull of the entire set S is composed of the upper and lower hulls, which can be constructed independently and in a similar fashion, is a very useful observation exploited by several algorithms for this problem.

For concreteness, let us discuss how quickhull proceeds to construct the upper hull; the lower hull can be constructed in the same manner. If S₁ is empty, the

upper hull is simply the line segment with the endpoints at p₁ and p_n. If S₁ is not empty, the algorithm identifies point p_max in S₁, which is the farthest from the line

Therefore, the algorithm can continue constructing the upper hulls of p₁ ∪ S_1,1 ∪ p_max and p_max ∪ S_1,2 ∪ p_n recursively and then simply concatenate them to get the upper hull of the entire set p₁ ∪ S₁ ∪ p_n.

Now we have to figure out how the algorithm’s geometric operations can be actually implemented. Fortunately, we can take advantage of the following very useful fact from analytical geometry: if q₁(x₁, y₁), q₂(x₂, y₂), and q₃(x₃, y₃) are three arbitrary points in the Cartesian plane, then the area of the triangle q₁q₂q₃ is equal to one-half of the magnitude of the determinant

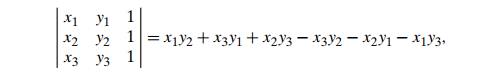
while the sign of this expression is positive if and only if the point q₃ = (x₃, y₃) is to

−−−→

the left of the line q₁ q₂ . Using this formula, we can check in constant time whether a point lies to the left of the line determined by two other points as well as find the distance from the point to the line.

Quickhull has the same  (n²) worst-case efficiency as quicksort (Problem 9 in this section’s exercises). In the average case, however, we should expect a much better performance. First, the algorithm should benefit from the quicksort-like savings from the on-average balanced split of the problem into two smaller subproblems. Second, a significant fraction of the points—namely, those inside p₁p_maxp_n (see Figure 5.9)—are eliminated from further processing. Under a natural assumption that points given are chosen randomly from a uniform dis-tribution over some convex region (e.g., a circle or a rectangle), the average-case efficiency of quickhull turns out to be linear [Ove80].

Exercises 5.5

                 a. For the one-dimensional version of the closest-pair problem, i.e., for the problem of finding two closest numbers among a given set of n real num-bers, design an algorithm that is directly based on the divide-and-conquer technique and determine its efficiency class.

b. Is it a good algorithm for this problem?

         Prove that the divide-and-conquer algorithm for the closest-pair problem examines, for every point p in the vertical strip (see Figures 5.7a and 5.7b), no more than seven other points that can be closer to p than d_min, the minimum distance between two points encountered by the algorithm up to that point.

         Consider the version of the divide-and-conquer two-dimensional closest-pair algorithm in which, instead of presorting input set P , we simply sort each of the two sets P_l and P_r in nondecreasing order of their y coordinates on each recursive call. Assuming that sorting is done by mergesort, set up a recurrence relation for the running time in the worst case and solve it for n = 2^k.

Implement the divide-and-conquer closest-pair algorithm, outlined in this section, in the language of your choice.

        Find on the Web a visualization of an algorithm for the closest-pair problem. What algorithm does this visualization represent?

        The Voronoi polygon for a point p of a set S of points in the plane is defined to be the perimeter of the set of all points in the plane closer to p than to any other point in S. The union of all the Voronoi polygons of the points in S is called the Voronoi diagram of S.

         What is the Voronoi diagram for a set of three points?

         Find a visualization of an algorithm for generating the Voronoi diagram on the Web and study a few examples of such diagrams. Based on your observations, can you tell how the solution to the previous question is generalized to the general case?

        Explain how one can find point p_max in the quickhull algorithm analytically.

        What is the best-case efficiency of quickhull?

        Give a specific example of inputs that make quickhull run in quadratic time.

            Implement quickhull in the language of your choice.

            Creating decagons There are 1000 points in the plane, no three of them on the same line. Devise an algorithm to construct 100 decagons with their vertices at these points. The decagons need not be convex, but each of them has to be simple, i.e., its boundary should not cross itself, and no two decagons may have a common point.

Shortest path around There is a fenced area in the two-dimensional Eu-clidean plane in the shape of a convex polygon with vertices at points p₁(x₁, y₁), p₂(x₂, y₂), . . . , p_n(x_n, y_n) (not necessarily in this order). There are two more points, a(x_a, y_a) and b(x_b, y_b) such that x_a < min{x₁, x₂, . . . , x_n} and x_b > max{x₁, x₂, . . . , x_n}. Design a reasonably efficient algorithm for comput-ing the length of the shortest path between a and b. [ORo98]