Binary Tree Traversals and Related Properties

                Binary Tree Traversals and Related Properties

In this section, we see how the divide-and-conquer technique can be applied to binary trees. A binary tree T is defined as a finite set of nodes that is either empty or consists of a root and two disjoint binary trees T_L and T_R called, respectively, the left and right subtree of the root. We usually think of a binary tree as a special case of an ordered tree (Figure 5.4). (This standard interpretation was an alternative definition of a binary tree in Section 1.4.)

Since the definition itself divides a binary tree into two smaller structures of the same type, the left subtree and the right subtree, many problems about binary trees can be solved by applying the divide-and-conquer technique. As an example, let us consider a recursive algorithm for computing the height of a binary tree. Recall that the height is defined as the length of the longest path from the root to a leaf. Hence, it can be computed as the maximum of the heights of the root’s left

and right subtrees plus 1. (We have to add 1 to account for the extra level of the root.) Also note that it is convenient to define the height of the empty tree as −1. Thus, we have the following recursive algorithm.

ALGORITHM     Height(T )

//Computes recursively the height of a binary tree //Input: A binary tree T

//Output: The height of T if T = ∅ return −1

else return max{Height(T_{lef t} ), Height(T_right )} + 1

We measure the problem’s instance size by the number of nodes n(T ) in a given binary tree T . Obviously, the number of comparisons made to compute the maximum of two numbers and the number of additions A(n(T )) made by the algorithm are the same. We have the following recurrence relation for A(n(T )):

A(n(T )) = A(n(T_{lef t} )) + A(n(T_right )) + 1  for n(T ) > 0,

A(0) = 0.

Before we solve this recurrence (can you tell what its solution is?), let us note that addition is not the most frequently executed operation of this algorithm. What is? Checking—and this is very typical for binary tree algorithms—that the tree is not empty. For example, for the empty tree, the comparison T = ∅ is executed once but there are no additions, and for a single-node tree, the comparison and addition numbers are 3 and 1, respectively.

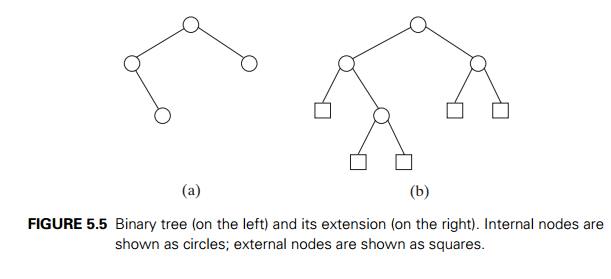
It helps in the analysis of tree algorithms to draw the tree’s extension by replacing the empty subtrees by special nodes. The extra nodes (shown by little squares in Figure 5.5) are called external; the original nodes (shown by little circles) are called internal. By definition, the extension of the empty binary tree is a single external node.

It is easy to see that the Height algorithm makes exactly one addition for every internal node of the extended tree, and it makes one comparison to check whether

the tree is empty for every internal and external node. Therefore, to ascertain the algorithm’s efficiency, we need to know how many external nodes an extended binary tree with n internal nodes can have. After checking Figure 5.5 and a few similar examples, it is easy to hypothesize that the number of external nodes x is always 1 more than the number of internal nodes n:

To prove this equality, consider the total number of nodes, both internal and external. Since every node, except the root, is one of the two children of an internal node, we have the equation

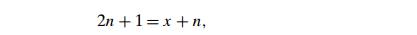
which immediately implies equality (5.2).

Note that equality (5.2) also applies to any nonempty full binary tree, in which, by definition, every node has either zero or two children: for a full binary tree, n and x denote the numbers of parental nodes and leaves, respectively.

Returning to algorithm Height, the number of comparisons to check whether the tree is empty is

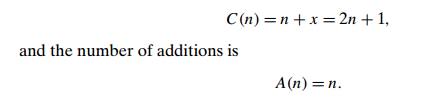
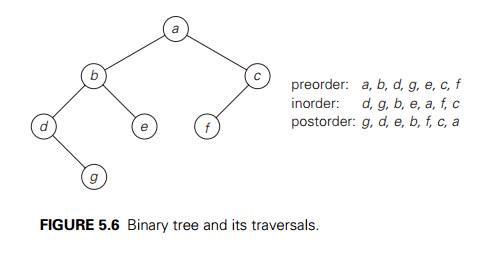
The most important divide-and-conquer algorithms for binary trees are the three classic traversals: preorder, inorder, and postorder. All three traversals visit nodes of a binary tree recursively, i.e., by visiting the tree’s root and its left and right subtrees. They differ only by the timing of the root’s visit:

In the preorder traversal, the root is visited before the left and right subtrees are visited (in that order).

In the inorder traversal, the root is visited after visiting its left subtree but before visiting the right subtree.

In the postorder traversal, the root is visited after visiting the left and right subtrees (in that order).

These traversals are illustrated in Figure 5.6. Their pseudocodes are quite straightforward, repeating the descriptions given above. (These traversals are also a standard feature of data structures textbooks.) As to their efficiency analysis, it is identical to the above analysis of the Height algorithm because a recursive call is made for each node of an extended binary tree.

Finally, we should note that, obviously, not all questions about binary trees require traversals of both left and right subtrees. For example, the search and insert operations for a binary search tree require processing only one of the two subtrees. Accordingly, we considered them in Section 4.5 not as applications of divide-and-conquer but rather as examples of the variable-size-decrease technique.

Exercises 5.3

         Design a divide-and-conquer algorithm for computing the number of levels in a binary tree. (In particular, the algorithm must return 0 and 1 for the empty and single-node trees, respectively.) What is the time efficiency class of your algorithm?

         The following algorithm seeks to compute the number of leaves in a binary tree.

ALGORITHM     LeafCounter(T )

//Computes recursively the number of leaves in a binary tree //Input: A binary tree T

//Output: The number of leaves in T if T = ∅ return 0

else return LeafCounter(T_{lef t} )+ LeafCounter(T_right )

Is this algorithm correct? If it is, prove it; if it is not, make an appropriate correction.

         Can you compute the height of a binary tree with the same asymptotic ef-ficiency as the section’s divide-and-conquer algorithm but without using a stack explicitly or implicitly? Of course, you may use a different algorithm altogether.

         Prove equality (5.2) by mathematical induction.

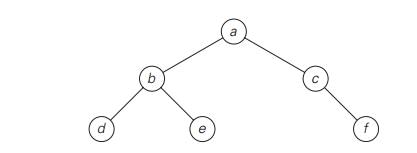
         Traverse the following binary tree

         in preorder.

         in inorder.

in postorder.

        Write pseudocode for one of the classic traversal algorithms (preorder, in-order, and postorder) for binary trees. Assuming that your algorithm is recur-sive, find the number of recursive calls made.

        Which of the three classic traversal algorithms yields a sorted list if applied to a binary search tree? Prove this property.

                 a. Draw a binary tree with 10 nodes labeled 0, 1, . . . , 9 in such a way that the inorder and postorder traversals of the tree yield the following lists: 9, 3, 1, 0, 4, 2, 7, 6, 8, 5 (inorder) and 9, 1, 4, 0, 3, 6, 7, 5, 8, 2 (postorder).

         Give an example of two permutations of the same n labels 0, 1, . . . , n − 1 that cannot be inorder and postorder traversal lists of the same binary tree.

         Design an algorithm that constructs a binary tree for which two given lists of n labels 0, 1, . . . , n − 1 are generated by the inorder and postorder traversals of the tree. Your algorithm should also identify inputs for which the problem has no solution.

        The internal path length I of an extended binary tree is defined as the sum of the lengths of the paths—taken over all internal nodes—from the root to each internal node. Similarly, the external path length E of an extended binary tree is defined as the sum of the lengths of the paths—taken over all external nodes—from the root to each external node. Prove that E = I + 2n where n is the number of internal nodes in the tree.

            Write a program for computing the internal path length of an extended binary tree. Use it to investigate empirically the average number of key comparisons for searching in a randomly generated binary search tree.

Chocolate bar puzzle Given an n × m chocolate bar, you need to break it into nm 1 × 1 pieces. You can break a bar only in a straight line, and only one bar can be broken at a time. Design an algorithm that solves the problem with the minimum number of bar breaks. What is this minimum number? Justify your answer by using properties of a binary tree.