The Closest Pair Problem by Divide and Conquer

                The Closest-Pair and Convex-Hull Problems by Divide-and-Conquer

In previews Section , we discussed the brute-force approach to solving two classic prob-lems of computational geometry: the closest-pair problem and the convex-hull problem. We saw that the two-dimensional versions of these problems can be solved by brute-force algorithms in  (n2) and O(n3) time, respectively. In this section, we discuss more sophisticated and asymptotically more efficient algorithms for these problems, which are based on the divide-and-conquer technique.

The Closest-Pair Problem

Let P be a set of n > 1 points in the Cartesian plane. For the sake of simplicity, we assume that the points are distinct. We can also assume that the points are ordered in nondecreasing order of their x coordinate. (If they were not, we could sort them first by an efficeint sorting algorithm such as mergesort.) It will also be convenient to have the points sorted in a separate list in nondecreasing order of the y coordinate; we will denote such a list Q.

If 2 ≤ n ≤ 3, the problem can be solved by the obvious brute-force algorithm. If n > 3, we can divide the points into two subsets P_l and P_r of n/2 and n/2 points, respectively, by drawing a vertical line through the median m of their x coordinates so that n/2 points lie to the left of or on the line itself, and n/2 points lie to the right of or on the line. Then we can solve the closest-pair problem

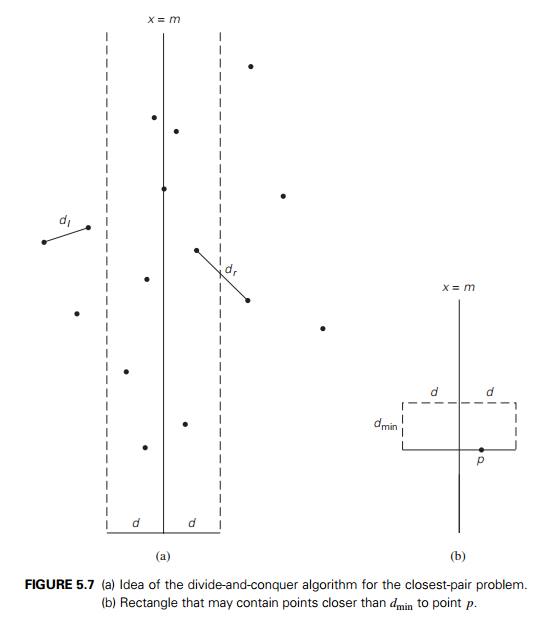
recursively for subsets P_l and P_r . Let d_l and d_r be the smallest distances between pairs of points in P_l and P_r , respectively, and let d = min{d_l, d_r }.

Note that d is not necessarily the smallest distance between all the point pairs because points of a closer pair can lie on the opposite sides of the separating line. Therefore, as a step combining the solutions to the smaller subproblems, we need to examine such points. Obviously, we can limit our attention to the points inside the symmetric vertical strip of width 2d around the separating line, since the distance between any other pair of points is at least d (Figure 5.7a).

Let S be the list of points inside the strip of width 2d around the separating line, obtained from Q and hence ordered in nondecreasing order of their y coor-dinate. We will scan this list, updating the information about d_min, the minimum distance seen so far, if we encounter a closer pair of points. Initially, d_min = d, and

subsequently d_min ≤ d. Let p(x, y) be a point on this list. For a point p (x , y ) to have a chance to be closer to p than d_min, the point must follow p on list S and the difference between their y coordinates must be less than d_min (why?). Geometri-

cally, this means that p must belong to the rectangle shown in Figure 5.7b. The principal insight exploited by the algorithm is the observation that the rectangle can contain just a few such points, because the points in each half (left and right) of the rectangle must be at least distance d apart. It is easy to prove that the total number of such points in the rectangle, including p, does not exceed eight (Prob-lem 2 in this section’s exercises); a more careful analysis reduces this number to six (see [Joh04, p. 695]). Thus, the algorithm can consider no more than five next points following p on the list S, before moving up to the next point.

Here is pseudocode of the algorithm. We follow the advice given in Section 3.3 to avoid computing square roots inside the innermost loop of the algorithm.

ALGORITHM                 EfficientClosestPair(P , Q)

//Solves the closest-pair problem by divide-and-conquer

//Input: An array P of n ≥ 2 points in the Cartesian plane sorted in

                        nondecreasing order of their x coordinates and an array Q of the

            same points sorted in nondecreasing order of the y coordinates //Output: Euclidean distance between the closest pair of points

if n ≤ 3

return the minimal distance found by the brute-force algorithm

else

copy the first n/2 points of P to array P_l copy the same n/2 points from Q to array Q_l copy the remaining n/2 points of P to array P_r copy the same n/2 points from Q to array Q_r d_l ← EfficientClosestPair(P_l, Q_l)

d_r ← EfficientClosestPair(P_r , Q_r )

d ←min{d_l, d_r }

m ← P [ n/2  − 1].x

copy all the points of Q for which |x − m| < d into array S[0..num − 1] dminsq ← d²

for i ← 0 to num − 2 do k ← i + 1

while k ≤ num − 1 and (S[k].y − S[i].y)² < dminsq

dminsq ← min((S[k].x − S[i].x)²+ (S[k].y − S[i].y)², dminsq) k ← k + 1

return sqrt(dminsq)

The algorithm spends linear time both for dividing the problem into two problems half the size and combining the obtained solutions. Therefore, assuming as usual that n is a power of 2, we have the following recurrence for the running time of the algorithm:

T (n) = 2T (n/2) + f (n),

where f (n) ∈  (n). Applying the Master Theorem (with a = 2, b = 2, and d = 1), we get T (n) ∈  (n log n). The necessity to presort input points does not change the overall efficiency class if sorting is done by a O(n log n) algorithm such as mergesort. In fact, this is the best efficiency class one can achieve, because it has been proved that any algorithm for this problem must be in  (n log n) under some natural assumptions about operations an algorithm can perform (see [Pre85, p. 188]).