Differential amplifier

Differential amplifier:

We will evaluate 2 different arrangements of the differential amplifier with -ve feedback. Classify these arrangements according to the number of op-amps used. i.e

1.        Differential amplifier with one op-amp

2.        Differential amplifier with two op-amps.

Differential amplifier are used in instrumentation and industrial applications to amplify differences between 2 input signals such as output of the wheat stone bridge circuit.

Differential amplifier preferred to these application because they are better able to reject common mode (noise) voltages than single input circuit such as inverting and non-inverting amplifier.

1. Differential Amplifier with one op-amp:

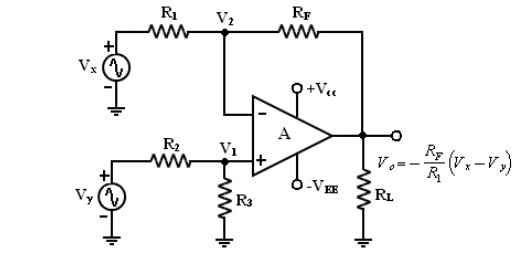
To analyse this circuit by deriving voltage gain and input resistance. This circuit is a combination of inverting and non-inverting amplifier. (i.e) WhenVx is reduced to zero the circuit is non-inverting amplifier and when Vy is reduced to zero the circuit is inverting amplifier.

Voltage Gain:

The circuit has 2 inputs Vx and Vy . Use superposition theorem, when Vy = 0V, becomes inverting amplifier. Hence the o/p due to Vx only is

Similarly, when Vx = 0V, becomes Non-inverting amplifier having a voltage divider network composed of R2 and R3 at the Non – inverting input.

Note : the gain of the differential amplifier is same as that of inverting amplifier.

Input Resistance:

The input resistance Rif of the differential amplifier is resistance determined looking into either one of the 2 input terminals with the other grounded,

With V_y = 0V,

Inverting amplifier, the input resistance which is,

R_iF_x ≈ R₁ -----------------

(26.a) Similarly, ,V_x = 0V,

Non-inverting amplifier, the input resistance which is,

R_iF_y ≈ (R₂ + R₃ ) ------(26.b)

V_x and V_y are not the same. Both the input resistance can be made equal, if we modify the basic differential amplifier. Both R₁ and (R₂ + R₃) can be made much larger than the source resistances. So that the loading of the signal sources does not occur.

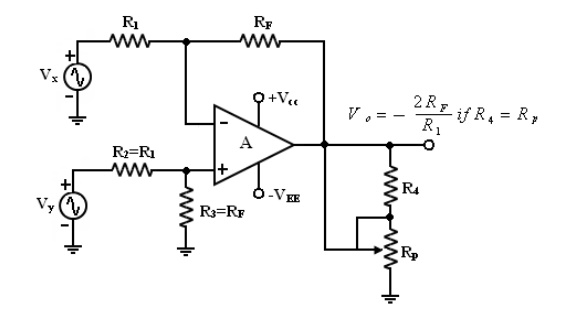
Note: If we need a variable gain, we can use the differential amplifier. In this circuit R₁ = R₂ , R_F = R₃ and the potentiometer R_p = R₄.

Depending on the position of the wiper in R voltage can be varied from the closed loop gain of - 2R_F /R₁ to the open loop gain of A.

2. Differential Amplifier with 2 op-amps:

We can increase the gain of the differential amplifier and also increase the input resistance Rif if we use 2 op-amps.

Voltage gain:

It is compares of 2 stages 

1. Non-inverting

2. Differential amplifier with gain.

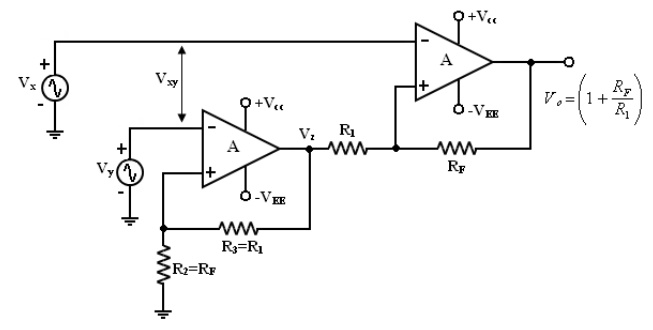
By finding the gain of these 2 stages, we can obtain the overall gain of the circuit,

Input Resistance:

The input resistance Rif of the differential amplifier is the resistance determined from either one of the two non-inverting terminals with the other grounded. The first stage A₁ is the non-inverting amplifier, its input resistance is

R_iF_y = R_i (1+AB) -----(29. a)

Where R_i = open loop input resistance of the op-amp.

B = R₂ /R₂ + R₃

Similarly, with V_y shorted to ground (V_y = 0 V), the 2^nd stage (A₂ ) also becomes non-inverting amplifier, whose input resistance is

RiFx = Ri (1+AB) -----(29. b)

Where R_i = open loop input resistance of the op-amp

B = R₁  /(R₁  + R_F)

Since R₁ = R₃ and RF = R₂ , the Rify ≠ RiFx because the loading of the input sources V_x and V_y may occur. (Or)

The output signal may be smaller in amplitude than expected. This possible reduction in the amplitude of the output signal is drawback of differential amplifier.

To overcome this:

With proper selection of components, both RiFy and RiFx can be made much larger than the sources resistance so that the loading of the input sources does not occur.

Output resistance and Bandwidth of differential amplifier with feedback:

The output resistance of the differential amplifier should be the same as that of the non-inverting amplifier expect that B = 1/AD (i.e)

A_D = closed loop gain of the differential amplifier

R0 = output resistance of the op-amp

A = open – loop volt gain of the op-amp

Remember that AD is different for differential amplifier.In the case of Inverting and Non-inverting amplifier, the bandwidth of the differential amplifier also depends on the closed loop gain of the amplifier and is given by,

f_F = Unity gain Bandwidth closed loop gain AD (or) fF = (A) (f0 )