Chapter: Introduction to the Design and Analysis of Algorithms : Decrease and Conquer
Decrease and Conquer
Decrease-and-Conquer
Plutarch says that Sertorius, in order to teach his
soldiers that perseverance and wit are better than brute force, had two horses
brought before them, and set two men to pull out their tails. One of the men
was a burly Hercules, who tugged and tugged, but all to no purpose; the other
was a sharp, weasel-faced tailor, who plucked one hair at a time, amidst roars
of laughter, and soon left the tail quite bare.
—E.
Cobham Brewer, Dictionary of Phrase and
Fable, 1898
The decrease-and-conquer technique is
based on exploiting the relationship between a solution to a given instance of
a problem and a solution to its smaller instance. Once such a relationship is
established, it can be exploited either top down or bottom up. The former leads
naturally to a recursive implementa-tion, although, as one can see from several
examples in this chapter, an ultimate implementation may well be nonrecursive.
The bottom-up variation is usually implemented iteratively, starting with a
solution to the smallest instance of the
problem;
it is called sometimes the incremental approach. There are
three major variations of decrease-and-conquer:
decrease
by a constant decrease by a constant factor variable size decrease
In the decrease-by-a-constant
variation, the size of an instance is reduced by the same constant on each
iteration of the algorithm. Typically, this constant is equal to one (Figure
4.1), although other constant size reductions do happen occasionally.
Consider, as an example, the exponentiation problem of computing an where a = 0 and n is a nonnegative integer. The relationship between a solution to an instance of size n and an instance of size n − 1 is obtained by the obvious formula an = an−1 . a. So the function f (n) = an can be computed either “top down” by using its recursive definition

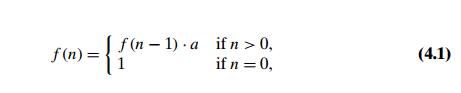
or
“bottom up” by multiplying 1 by a n times.
(Yes, it is the same as the brute-force algorithm, but we have come to it by a
different thought process.) More interesting examples of decrease-by-one
algorithms appear in Sections 4.1–4.3.
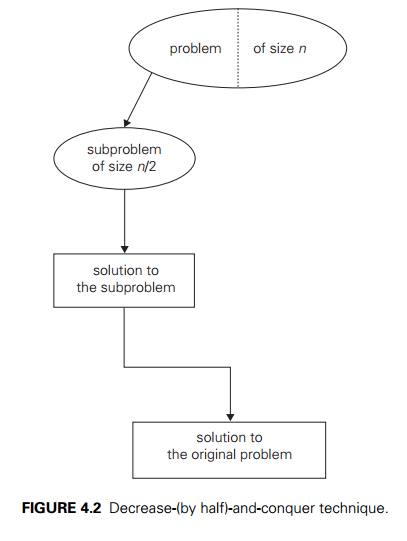
The decrease-by-a-constant-factor
technique suggests reducing a problem instance by the same constant factor on
each iteration of the algorithm. In most applications, this constant factor is
equal to two. (Can you give an example of such an algorithm?) The
decrease-by-half idea is illustrated in Figure 4.2.
For an
example, let us revisit the exponentiation problem. If the instance of size n is to compute an, the
instance of half its size is to compute an/2, with
the obvious relationship between the two: an = (an/2)2. But since we consider here
instances with integer exponents only, the former does not work for odd n. If n is odd,
we have to compute an−1 by using
the rule for even-valued exponents and then multiply the result by a. To summarize, we have the
following formula:
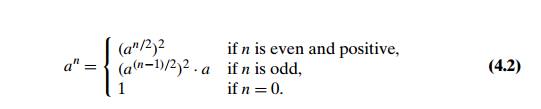
If we
compute an
recursively according to formula (4.2) and measure the algo-rithm’s efficiency
by the number of multiplications, we should expect the algorithm to be in (log n) because, on each iteration, the
size is reduced by about a half at the expense of one or two multiplications.
A few
other examples of decrease-by-a-constant-factor algorithms are given in Section
4.4 and its exercises. Such algorithms are so efficient, however, that there
are few examples of this kind.
Finally,
in the variable-size-decrease variety of decrease-and-conquer, the
size-reduction pattern varies from one iteration of an algorithm to another.
Eu-clid’s algorithm for computing the greatest common divisor provides a good
ex-ample of such a situation. Recall that this algorithm is based on the
formula
gcd(m, n) = gcd(n, m mod n).
Though
the value of the second argument is always smaller on the right-hand side than
on the left-hand side, it decreases neither by a constant nor by a constant
factor. A few other examples of such algorithms appear in Section 4.5.
Related Topics