Algorithms for Generating Combinatorial Objects

Algorithms for Generating Combinatorial Objects

1. Generating Permutations

2. Generating Subsets

3. Exercises

In this section, we keep our promise to discuss algorithms for generating combi-natorial objects. The most important types of combinatorial objects are permuta-tions, combinations, and subsets of a given set. They typically arise in problems that require a consideration of different choices. We already encountered them in Chapter 3 when we discussed exhaustive search. Combinatorial objects are stud-ied in a branch of discrete mathematics called combinatorics. Mathematicians, of course, are primarily interested in different counting formulas; we should be grate-ful for such formulas because they tell us how many items need to be generated. In particular, they warn us that the number of combinatorial objects typically grows exponentially or even faster as a function of the problem size. But our primary interest here lies in algorithms for generating combinatorial objects, not just in counting them.

Generating Permutations

We start with permutations. For simplicity, we assume that the underlying set whose elements need to be permuted is simply the set of integers from 1 to n; more generally, they can be interpreted as indices of elements in an n-element set {a₁, . . . , a_n}. What would the decrease-by-one technique suggest for the problem of generating all n! permutations of {1, . . . , n}? The smaller-by-one problem is to generate all (n − 1)! permutations. Assuming that the smaller problem is solved, we can get a solution to the larger one by inserting n in each of the n possible positions among elements of every permutation of n − 1 elements. All the permu-tations obtained in this fashion will be distinct (why?), and their total number will be n(n − 1)! = n!. Hence, we will obtain all the permutations of {1, . . . , n}.

We can insert n in the previously generated permutations either left to right or right to left. It turns out that it is beneficial to start with inserting n into 12 . . . (n − 1) by moving right to left and then switch direction every time a new permutation of {1, . . . , n − 1} needs to be processed. An example of applying this approach bottom up for n = 3 is given in Figure 4.9.

The advantage of this order of generating permutations stems from the fact that it satisfies the minimal-change requirement: each permutation can be ob-tained from its immediate predecessor by exchanging just two elements in it. (For the method being discussed, these two elements are always adjacent to each other.

Check this for the permutations generated in Figure 4.9.) The minimal-change re-quirement is beneficial both for the algorithm’s speed and for applications using the permutations. For example, in Section 3.4, we needed permutations of cities to solve the traveling salesman problem by exhaustive search. If such permuta-tions are generated by a minimal-change algorithm, we can compute the length of a new tour from the length of its predecessor in constant rather than linear time (how?).

It is possible to get the same ordering of permutations of n elements without explicitly generating permutations for smaller values of n. It can be done by associating a direction with each element k in a permutation. We indicate such a direction by a small arrow written above the element in question, e.g.,

3 and 4 are mobile while 2 and 1 are not. Using the notion of a mobile element, we can give the following description of the Johnson-Trotter algorithm for generating permutations.

ALGORITHM     JohnsonTrotter(n)

//Implements Johnson-Trotter algorithm for generating permutations //Input: A positive integer n

//Output: A list of all permutations of {1, . . . , n}

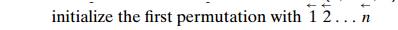
while the last permutation has a mobile element do find its largest mobile element k

swap k with the adjacent element k’s arrow points to

reverse the direction of all the elements that are larger than k add the new permutation to the list

Here is an application of this algorithm for n = 3, with the largest mobile element shown in bold:

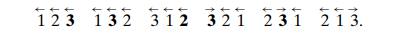
This algorithm is one of the most efficient for generating permutations; it can be implemented to run in time proportional to the number of permutations, i.e., in  (n!). Of course, it is horribly slow for all but very small values of n; however, this is not the algorithm’s “fault” but rather the fault of the problem: it simply asks to generate too many items.

One can argue that the permutation ordering generated by the Johnson-Trotter algorithm is not quite natural; for example, the natural place for permu-tation n(n − 1) . . . 1 seems to be the last one on the list. This would be the case if permutations were listed in increasing order—also called the lexicographic or- der—which is the order in which they would be listed in a dictionary if the numbers were interpreted as letters of an alphabet. For example, for n = 3,

123 132 213 231 312 321.

So how can we generate the permutation following a₁a₂ . . . a_n−1a_n in lexi-cographic order? If a_n−1 < a_n, which is the case for exactly one half of all the permutations, we can simply transpose these last two elements. For example, 123 is followed by 132. If a_n−1 > a_n, we find the permutation’s longest decreasing suffix a_i+1 > a_{i +2} > ^{. . .} > a_n (but a_i < a_i+1); increase a_i by exchanging it with the smallest element of the suffix that is greater than a_i; and reverse the new suffix to put it in increasing order. For example, 362541 is followed by 364125. Here is pseudocode of this simple algorithm whose origins go as far back as 14th-century India.

ALGORITHM                 LexicographicPermute(n)

//Generates permutations in lexicographic order //Input: A positive integer n

//Output: A list of all permutations of {1, . . . , n} in lexicographic order initialize the first permutation with 12 . . . n

while last permutation has two consecutive elements in increasing order do

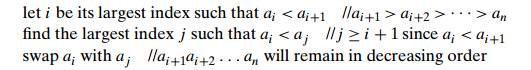
reverse the order of the elements from a_i+1 to a_n inclusive

add the new permutation to the list

Generating Subsets

Recall that in Section 3.4 we examined the knapsack problem, which asks to find the most valuable subset of items that fits a knapsack of a given capacity. The exhaustive-search approach to solving this problem discussed there was based on generating all subsets of a given set of items. In this section, we discuss algorithms for generating all 2ⁿ subsets of an abstract set A = {a₁, . . . , a_n}. (Mathematicians call the set of all subsets of a set its power set.)

The decrease-by-one idea is immediately applicable to this problem, too. All subsets of A = {a₁, . . . , a_n} can be divided into two groups: those that do not contain a_n and those that do. The former group is nothing but all the subsets of {a₁, . . . , a_n−1}, while each and every element of the latter can be obtained by adding a_n to a subset of {a₁, . . . , a_n−1}. Thus, once we have a list of all subsets of {a₁, . . . , a_n−1}, we can get all the subsets of {a₁, . . . , a_n} by adding to the list all its elements with a_n put into each of them. An application of this algorithm to generate all subsets of {a₁, a₂, a₃} is illustrated in Figure 4.10.

Similarly to generating permutations, we do not have to generate power sets of smaller sets. A convenient way of solving the problem directly is based on a one-to-one correspondence between all 2ⁿ subsets of an n element set A = {a₁, . . . , a_n}

and all 2ⁿ bit strings b₁, . . . , b_n of length n. The easiest way to establish such a correspondence is to assign to a subset the bit string in which b_i = 1 if a_i belongs to the subset and b_i = 0 if a_i does not belong to it. (We mentioned this idea of bit vectors in Section 1.4.) For example, the bit string 000 will correspond to the empty subset of a three-element set, 111 will correspond to the set itself, i.e., {a₁, a₂, a₃}, and 110 will represent {a₁, a₂}. With this correspondence in place, we can generate all the bit strings of length n by generating successive binary numbers from 0 to 2ⁿ − 1, padded, when necessary, with an appropriate number of leading 0’s. For example, for the case of n = 3, we obtain

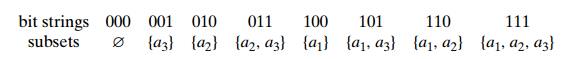
Note that although the bit strings are generated by this algorithm in lexico-graphic order (in the two-symbol alphabet of 0 and 1), the order of the subsets looks anything but natural. For example, we might want to have the so-called squashed order, in which any subset involving a_j can be listed only after all the subsets involving a₁, . . . , a_{j −1}, as was the case for the list of the three-element set in Figure 4.10. It is easy to adjust the bit string–based algorithm above to yield a squashed ordering of the subsets involved (see Problem 6 in this section’s exer-cises).

A more challenging question is whether there exists a minimal-change algo-rithm for generating bit strings so that every one of them differs from its immediate predecessor by only a single bit. (In the language of subsets, we want every subset to differ from its immediate predecessor by either an addition or a deletion, but not both, of a single element.) The answer to this question is yes. For example, for n = 3, we can get

000                     001 011 010 110 111 101 100.

Such a sequence of bit strings is called the binary reflected Gray code. Frank Gray, a researcher at AT&T Bell Laboratories, reinvented it in the 1940s to minimize the effect of errors in transmitting digital signals (see, e.g., [Ros07], pp. 642–

´

643). Seventy years earlier, the French engineer Emile Baudot used such codes in telegraphy. Here is pseudocode that generates the binary reflected Gray code recursively.

ALGORITHM                 BRGC(n)

//Generates recursively the binary reflected Gray code of order n //Input: A positive integer n

//Output: A list of all bit strings of length n composing the Gray code if n = 1 make list L containing bit strings 0 and 1 in this order

else generate list L1 of bit strings of size n − 1 by calling BRGC(n − 1) copy list L1 to list L2 in reversed order

add 0 in front of each bit string in list L1 add 1 in front of each bit string in list L2 append L2 to L1 to get list L

return L

The correctness of the algorithm stems from the fact that it generates 2ⁿ bit strings and all of them are distinct. Both these assertions are easy to check by mathematical induction. Note that the binary reflected Gray code is cyclic: its last bit string differs from the first one by a single bit. For a nonrecursive algorithm for generating the binary reflected Gray code see Problem 9 in this section’s exercises.

Exercises 4.3

            Is it realistic to implement an algorithm that requires generating all permu-tations of a 25-element set on your computer? What about all the subsets of such a set?

            Generate all permutations of {1, 2, 3, 4} by

            the bottom-up minimal-change algorithm.

            the Johnson-Trotter algorithm.

            the lexicographic-order algorithm.

            Apply LexicographicPermute to multiset {1, 2, 2, 3}. Does it generate correctly all the permutations in lexicographic order?

            Consider the following implementation of the algorithm for generating per-mutations discovered by B. Heap [Hea63].

ALGORITHM                      HeapPermute(n)

//Implements Heap’s algorithm for generating permutations

 //Input: A positive integer n and a global array A[1..n]

//Output: All permutations of elements of A

if n = 1 write A

else

for i ← 1 to n do

HeapPermute(n − 1)

if n is odd

swap A[1] and A[n] else swap A[i] and A[n]

            Trace the algorithm by hand for n = 2, 3, and 4.

            Prove the correctness of Heap’s algorithm.

            What is the time efficiency of HeapPermute?

            Generate all the subsets of a four-element set A = {a₁, a₂, a₃, a₄} by each of the two algorithms outlined in this section.

            What simple trick would make the bit string–based algorithm generate subsets in squashed order?

            Write pseudocode for a recursive algorithm for generating all 2ⁿ bit strings of length n.

            Write a nonrecursive algorithm for generating 2ⁿ bit strings of length n that implements bit strings as arrays and does not use binary additions.

            a.  Generate the binary reflexive Gray code of order 4.

            Trace the following nonrecursive algorithm to generate the binary re-flexive Gray code of order 4. Start with the n-bit string of all 0’s. For i = 1, 2, . . . , 2ⁿ⁻¹, generate the ith bit string by flipping bit b in the previ-ous bit string, where b is the position of the least significant 1 in the binary representation of i.

            Design a decrease-and-conquer algorithm for generating all combinations of k items chosen from n, i.e., all k-element subsets of a given n-element set. Is your algorithm a minimal-change algorithm?

            Gray code and the Tower of Hanoi

            Show that the disk moves made in the classic recursive algorithm for the Tower of Hanoi puzzle can be used for generating the binary reflected Gray code.

            Show how the binary reflected Gray code can be used for solving the Tower of Hanoi puzzle.

Fair attraction In olden days, one could encounter the following attraction at a fair. A light bulb was connected to several switches in such a way that it lighted up only when all the switches were closed. Each switch was controlled by a push button; pressing the button toggled the switch, but there was no way to know the state of the switch. The object was to turn the light bulb on. Design an algorithm to turn on the light bulb with the minimum number of button pushes needed in the worst case for n switches.