Decrease by a Constant Factor Algorithms

Decrease-by-a-Constant-Factor Algorithms

1. Binary Search

2. Fake-Coin Problem

3. Russian Peasant Multiplication

4. Josephus Problem

5. Exercises

You may recall from the introduction to this chapter that decrease-by-a-constant-factor is the second major variety of decrease-and-conquer. As an example of an algorithm based on this technique, we mentioned there exponentiation by squar-ing defined by formula (4.2). In this section, you will find a few other examples of such algorithms.. The most important and well-known of them is binary search. Decrease-by-a-constant-factor algorithms usually run in logarithmic time, and, be-ing very efficient, do not happen often; a reduction by a factor other than two is especially rare.

Binary Search

Binary search is a remarkably efficient algorithm for searching in a sorted array. It works by comparing a search key K with the array’s middle element A[m]. If they match, the algorithm stops; otherwise, the same operation is repeated recursively for the first half of the array if K < A[m], and for the second half if K > A[m]:

Though binary search is clearly based on a recursive idea, it can be easily implemented as a nonrecursive algorithm, too. Here is pseudocode of this nonre-cursive version.

ALGORITHM     BinarySearch(A[0..n − 1], K)

//Implements nonrecursive binary search

//Input: An array A[0..n − 1] sorted in ascending order and

            a search key K

//Output: An index of the array’s element that is equal to K

//            or −1 if there is no such element

l ← 0;     r ← n − 1

while l ≤ r do

m ←  (l + r)/2

if K = A[m] return m

else if K < A[m] r ← m − 1 else l ← m + 1

return −1

The standard way to analyze the efficiency of binary search is to count the number of times the search key is compared with an element of the array. Moreover, for the sake of simplicity, we will count the so-called three-way comparisons. This assumes that after one comparison of K with A[m], the algorithm can determine whether K is smaller, equal to, or larger than A[m].

How many such comparisons does the algorithm make on an array of n elements? The answer obviously depends not only on n but also on the specifics of a particular instance of the problem. Let us find the number of key comparisons

in the worst case C_worst (n). The worst-case inputs include all arrays that do not contain a given search key, as well as some successful searches. Since after one

comparison the algorithm faces the same situation but for an array half the size, we get the following recurrence relation for C_worst (n):

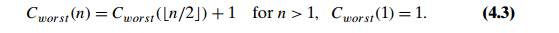
(Stop and convince yourself that n/2 must be, indeed, rounded down and that the initial condition must be written as specified.)

We already encountered recurrence (4.3), with a different initial condition, in Section 2.4 (see recurrence (2.4) and its solution there for n = 2^k). For the initial condition C_worst (1) = 1, we obtain

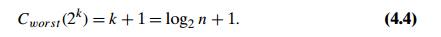
Further, similarly to the case of recurrence (2.4) (Problem 7 in Exercises 2.4), the solution given by formula (4.4) for n = 2^k can be tweaked to get a solution valid for an arbitrary positive integer n:

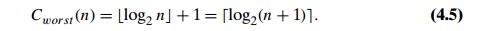
Formula (4.5) deserves attention. First, it implies that the worst-case time efficiency of binary search is in  (log n). Second, it is the answer we should have fully expected: since the algorithm simply reduces the size of the remaining array by about half on each iteration, the number of such iterations needed to reduce the initial size n to the final size 1 has to be about log₂ n. Third, to reiterate the point made in Section 2.1, the logarithmic function grows so slowly that its values remain small even for very large values of n. In particular, according to formula (4.5), it will take no more than log₂(10³ + 1) = 10 three-way comparisons to find an element of a given value (or establish that there is no such element) in any sorted array of one thousand elements, and it will take no more than log₂(10⁶ + 1) = 20 comparisons to do it for any sorted array of size one million!

What can we say about the average-case efficiency of binary search? A so-phisticated analysis shows that the average number of key comparisons made by binary search is only slightly smaller than that in the worst case:

C_avg(n) ≈ log₂ n.

(More accurate formulas for the average number of comparisons in a successful and an unsuccessful search are C_avg^yes(n) ≈ log₂ n − 1 and C_avg^no(n) ≈ log₂(n + 1), respectively.)

Though binary search is an optimal searching algorithm if we restrict our op-erations only to comparisons between keys (see Section 11.2), there are searching algorithms (see interpolation search in Section 4.5 and hashing in Section 7.3) with a better average-case time efficiency, and one of them (hashing) does not even re-quire the array to be sorted! These algorithms do require some special calculations in addition to key comparisons, however. Finally, the idea behind binary search has several applications beyond searching (see, e.g., [Ben00]). In addition, it can be applied to solving nonlinear equations in one unknown; we discuss this continuous analogue of binary search, called the method of bisection, in Section 12.4.

Fake-Coin Problem

Of several versions of the fake-coin identification problem, we consider here the one that best illustrates the decrease-by-a-constant-factor strategy. Among n identical-looking coins, one is fake. With a balance scale, we can compare any two sets of coins. That is, by tipping to the left, to the right, or staying even, the balance scale will tell whether the sets weigh the same or which of the sets is heavier than the other but not by how much. The problem is to design an efficient algorithm for detecting the fake coin. An easier version of the problem—the one we discuss here—assumes that the fake coin is known to be, say, lighter than the genuine one.¹

The most natural idea for solving this problem is to divide n coins into two piles of n/2 coins each, leaving one extra coin aside if n is odd, and put the two

piles on the scale. If the piles weigh the same, the coin put aside must be fake; otherwise, we can proceed in the same manner with the lighter pile, which must be the one with the fake coin.

We can easily set up a recurrence relation for the number of weighings W (n) needed by this algorithm in the worst case:

W (n) = W ( n/2 ) + 1             for n > 1,    W (1) = 0.

This recurrence should look familiar to you. Indeed, it is almost identical to the one for the worst-case number of comparisons in binary search. (The difference is in the initial condition.) This similarity is not really surprising, since both algorithms are based on the same technique of halving an instance size. The solution to the recurrence for the number of weighings is also very similar to the one we had for binary search: W (n) = log₂ n .

This stuff should look elementary by now, if not outright boring. But wait: the interesting point here is the fact that the above algorithm is not the most efficient solution. It would be more efficient to divide the coins not into two but into three piles of about n/3 coins each. (Details of a precise formulation are developed in this section’s exercises. Do not miss it! If your instructor forgets, demand the instructor to assign Problem 10.) After weighing two of the piles, we can reduce the instance size by a factor of three. Accordingly, we should expect the number of weighings to be about log₃ n, which is smaller than log₂ n.

Russian Peasant Multiplication

Now we consider a nonorthodox algorithm for multiplying two positive integers called multiplication a` la russe or the Russian peasant method . Let n and m be positive integers whose product we want to compute, and let us measure the instance size by the value of n. Now, if n is even, an instance of half the size has to deal with n/2, and we have an obvious formula relating the solution to the problem’s larger instance to the solution to the smaller one:

Using these formulas and the trivial case of 1 ^. m = m to stop, we can compute product n ^. m either recursively or iteratively. An example of computing 50 ^. 65 with this algorithm is given in Figure 4.11. Note that all the extra addends shown in parentheses in Figure 4.11a are in the rows that have odd values in the first column. Therefore, we can find the product by simply adding all the elements in the m column that have an odd number in the n column (Figure 4.11b).

Also note that the algorithm involves just the simple operations of halving, doubling, and adding—a feature that might be attractive, for example, to those

who do not want to memorize the table of multiplications. It is this feature of the algorithm that most probably made it attractive to Russian peasants who, accord-ing to Western visitors, used it widely in the nineteenth century and for whom the method is named. (In fact, the method was known to Egyptian mathematicians as early as 1650 B.C. [Cha98, p. 16].) It also leads to very fast hardware implementa-tion since doubling and halving of binary numbers can be performed using shifts, which are among the most basic operations at the machine level.

Josephus Problem

Our last example is the Josephus problem, named for Flavius Josephus, a famous Jewish historian who participated in and chronicled the Jewish revolt of 66–70 C.E. against the Romans. Josephus, as a general, managed to hold the fortress of Jotapata for 47 days, but after the fall of the city he took refuge with 40 diehards in a nearby cave. There, the rebels voted to perish rather than surrender. Josephus proposed that each man in turn should dispatch his neighbor, the order to be determined by casting lots. Josephus contrived to draw the last lot, and, as one of the two surviving men in the cave, he prevailed upon his intended victim to surrender to the Romans.

So let n people numbered 1 to n stand in a circle. Starting the grim count with person number 1, we eliminate every second person until only one survivor is left. The problem is to determine the survivor’s number J (n). For example (Figure 4.12), if n is 6, people in positions 2, 4, and 6 will be eliminated on the first pass through the circle, and people in initial positions 3 and 1 will be eliminated on the second pass, leaving a sole survivor in initial position 5—thus, J (6) = 5. To give another example, if n is 7, people in positions 2, 4, 6, and 1 will be eliminated on the first pass (it is more convenient to include 1 in the first pass) and people in positions 5 and, for convenience, 3 on the second—thus, J (7) = 7.

It is convenient to consider the cases of even and odd n’s separately. If n is even, i.e., n = 2k, the first pass through the circle yields an instance of exactly the same problem but half its initial size. The only difference is in position numbering; for example, a person in initial position 3 will be in position 2 for the second pass, a person in initial position 5 will be in position 3, and so on (check Figure 4.12a). It is easy to see that to get the initial position of a person, we simply need to multiply his new position by 2 and subtract 1. This relationship will hold, in particular, for the survivor, i.e.,

J (2k) = 2J (k) − 1.

Let us now consider the case of an odd n (n > 1), i.e., n = 2k + 1. The first pass eliminates people in all even positions. If we add to this the elimination of the person in position 1 right after that, we are left with an instance of size k. Here, to get the initial position that corresponds to the new position numbering, we have to multiply the new position number by 2 and add 1 (check Figure 4.12b). Thus, for odd values of n, we get

J (2k + 1) = 2J (k) + 1.

Can we get a closed-form solution to the two-case recurrence subject to the initial condition J (1) = 1? The answer is yes, though getting it requires more ingenuity than just applying backward substitutions. In fact, one way to find a solution is to apply forward substitutions to get, say, the first 15 values of J (n), discern a pattern, and then prove its general validity by mathematical induction. We leave the execution of this plan to the exercises; alternatively, you can look it up in [GKP94], whose exposition of the Josephus problem we have been following. Interestingly, the most elegant form of the closed-form answer involves the binary representation of size n: J (n) can be obtained by a 1-bit cyclic shift left of n itself! For example, J (6) = J (110₂) = 101₂ = 5 and J (7) = J (111₂) = 111₂ = 7.

Exercises 4.4

            1. Cutting a stick A stick n inches long needs to be cut into n 1-inch pieces. Outline an algorithm that performs this task with the minimum number of 1. cuts if several pieces of the stick can be cut at the same time. Also give a formula for the minimum number of cuts.

           2. Design a decrease-by-half algorithm for computing log₂ n and determine its time efficiency.

            3. a. What is the largest number of key comparisons made by binary search in searching for a key in the following array?

            List all the keys of this array that will require the largest number of key comparisons when searched for by binary search.

            Find the average number of key comparisons made by binary search in a successful search in this array. Assume that each key is searched for with the same probability.

            Find the average number of key comparisons made by binary search in an unsuccessful search in this array. Assume that searches for keys in each of the 14 intervals formed by the array’s elements are equally likely.

         4.    Estimate how many times faster an average successful search will be in a sorted array of one million elements if it is done by binary search versus sequential search.

         5.    The time efficiency of sequential search does not depend on whether a list is implemented as an array or as a linked list. Is it also true for searching a sorted list by binary search?

            6. a. Design a version of binary search that uses only two-way comparisons such as ≤ and =. Implement your algorithm in the language of your choice and carefully debug it: such programs are notorious for being prone to bugs.

            Analyze the time efficiency of the two-way comparison version designed in part a.

           7. Picture guessing A version of the popular problem-solving task involves pre-senting people with an array of 42 pictures—seven rows of six pictures each— and asking them to identify the target picture by asking questions that can be answered yes or no. Further, people are then required to identify the picture with as few questions as possible. Suggest the most efficient algorithm for this problem and indicate the largest number of questions that may be necessary.

8. Consider ternary search—the following algorithm for searching in a sorted array A[0..n − 1]. If n = 1, simply compare the search key K with the single element of the array; otherwise, search recursively by comparing K with A[ n/3 ], and if K is larger, compare it with A[ 2n/3 ] to determine in which third of the array to continue the search.

            What design technique is this algorithm based on?

            Set up a recurrence for the number of key comparisons in the worst case. You may assume that n = 3^k.

            Solve the recurrence for n = 3^k.

            Compare this algorithm’s efficiency with that of binary search.

         9.    An array A[0..n − 2] contains n − 1 integers from 1 to n in increasing order. (Thus one integer in this range is missing.) Design the most efficient algorithm you can to find the missing integer and indicate its time efficiency.

            10. a. Write pseudocode for the divide-into-three algorithm for the fake-coin problem. Make sure that your algorithm handles properly all values of n, not only those that are multiples of 3.

            Set up a recurrence relation for the number of weighings in the divide-into-three algorithm for the fake-coin problem and solve it for n = 3^k.

            For large values of n, about how many times faster is this algorithm than the one based on dividing coins into two piles? Your answer should not depend on n.

           11. a.  Apply the Russian peasant algorithm to compute 26 ^. 47.

            From the standpoint of time efficiency, does it matter whether we multiply n by m or m by n by the Russian peasant algorithm?

       12.      a.  Write pseudocode for the Russian peasant multiplication algorithm.

            What is the time efficiency class of Russian peasant multiplication?

       13.      Find J (40)—the solution to the Josephus problem for n = 40.

         14.    Prove that the solution to the Josephus problem is 1 for every n that is a power of 2.

           15.  For the Josephus problem,

            compute J (n) for n = 1, 2, . . . , 15.

            discern a pattern in the solutions for the first fifteen values of n and prove its general validity.

            prove the validity of getting J (n) by a 1-bit cyclic shift left of the binary representation of n.