Chapter: Introduction to the Design and Analysis of Algorithms : Decrease and Conquer
Topological Sorting
Topological
Sorting
In this
section, we discuss an important problem for directed graphs, with a variety of
applications involving prerequisite-restricted tasks. Before we pose this
problem, though, let us review a few basic facts about directed graphs
themselves. A directed graph, or digraph for short, is a graph with
directions specified for all its edges (Figure 4.5a is an example). The
adjacency matrix and adjacency lists are still two principal means of
representing a digraph. There are only two notable differences between
undirected and directed graphs in representing them: (1) the adjacency matrix
of a directed graph does not have to be symmetric; (2) an edge in a directed
graph has just one (not two) corresponding nodes in the digraph’s adjacency
lists.
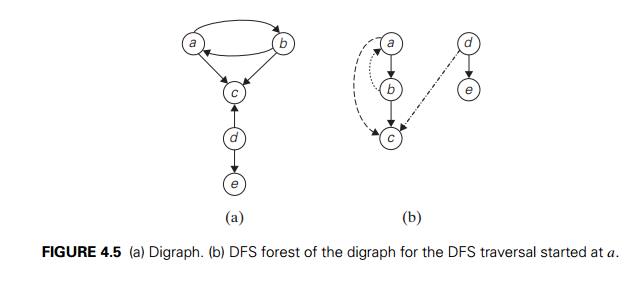
Depth-first
search and breadth-first search are principal traversal algorithms for
traversing digraphs as well, but the structure of corresponding forests can be
more complex than for undirected graphs. Thus, even for the simple example of
Figure 4.5a, the depth-first search forest (Figure 4.5b) exhibits all four
types of edges possible in a DFS forest of a directed graph: tree
edges (ab, bc, de), back edges (ba) from
vertices to their ancestors, forward edges (ac) from
vertices to their descendants in the tree other than their children, and cross
edges (dc), which
are none of the aforementioned types.
Note that
a back edge in a DFS forest of a directed graph can connect a vertex to its
parent. Whether or not it is the case, the presence of a back edge indicates
that the digraph has a directed cycle. A directed cycle in a digraph is a
sequence of three or more of its vertices that starts and ends with the same
vertex and in which every vertex is connected to its immediate predecessor by
an edge directed from the predecessor to the successor. For example, a, b, a is a directed cycle in the
digraph in Figure 4.5a. Conversely, if a DFS forest of a digraph has no back
edges, the digraph is a dag, an acronym for directed
acyclic graph.
Edge
directions lead to new questions about digraphs that are either meaning-less or
trivial for undirected graphs. In this section, we discuss one such question.
As a motivating example, consider a set of five required courses {C1, C2, C3,
C4, C5} a part-time student has to take in some degree program. The courses can
be taken in any order as long as the following course prerequisites are met: C1
and C2 have no prerequisites, C3 requires C1 and C2, C4 requires C3, and C5
requires C3 and C4. The student can take only one course per term. In which
order should the student take the courses?
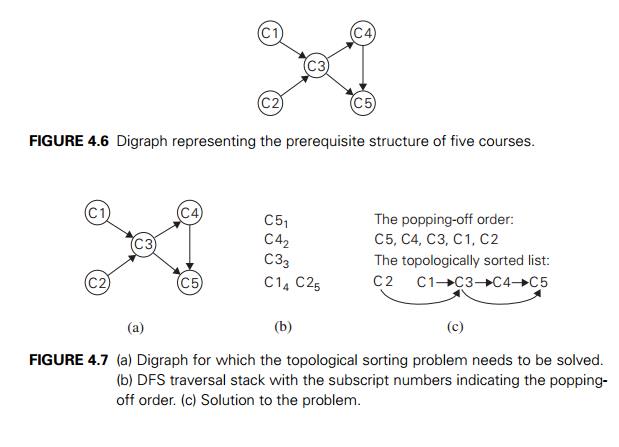
The
situation can be modeled by a digraph in which vertices represent courses and
directed edges indicate prerequisite requirements (Figure 4.6). In terms of
this digraph, the question is whether we can list its vertices in such an order
that for every edge in the graph, the vertex where the edge starts is listed
before the vertex where the edge ends. (Can you
find such an ordering of this digraph’s vertices?) This problem is called topological
sorting. It can be posed for an
arbitrary
digraph, but it is easy to see that the problem cannot have a solution if a
digraph has a directed cycle. Thus, for topological sorting to be possible, a
digraph in question must be a dag. It turns out that being a dag is not only
necessary but also sufficient for topological sorting to be possible; i.e., if
a digraph has no directed cycles, the topological sorting problem for it has a
solution. Moreover, there are two efficient algorithms that both verify whether
a digraph is a dag and, if it is, produce an ordering of vertices that solves
the topological sorting problem.
The first
algorithm is a simple application of depth-first search: perform a DFS
traversal and note the order in which vertices become dead-ends (i.e., popped
off the traversal stack). Reversing this order yields a solution to the
topological sorting problem, provided, of course, no back edge has been
encountered during the traversal. If a back edge has been encountered, the
digraph is not a dag, and topological sorting of its vertices is impossible.
Why does
the algorithm work? When a vertex v is
popped off a DFS stack, no vertex u with an
edge from u to v can be
among the vertices popped off before v.
(Otherwise, (u, v) would have been a back edge.)
Hence, any such vertex u will be listed after v in the popped-off order list,
and before v in the reversed list.
Figure
4.7 illustrates an application of this algorithm to the digraph in Fig-ure 4.6.
Note that in Figure 4.7c, we have drawn the edges of the digraph, and they all
point from left to right as the problem’s statement requires. It is a
con-venient way to check visually the correctness of a solution to an instance
of the topological sorting problem.
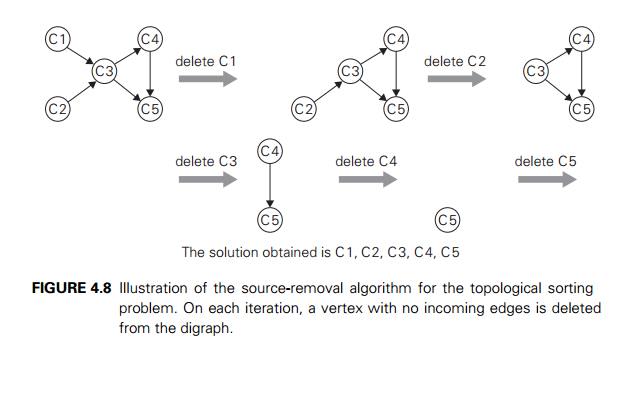
The
second algorithm is based on a direct implementation of the decrease-(by
one)-and-conquer technique: repeatedly, identify in a remaining digraph a source,
which is a vertex with no incoming edges, and delete it along with all the
edges outgoing from it. (If there are several sources, break the tie
arbitrarily. If there are none, stop because the problem cannot be solved—see
Problem 6a in this section’s exercises.) The order in which the vertices are
deleted yields a solution to the topological sorting problem. The application
of this algorithm to the same digraph representing the five courses is given in
Figure 4.8.
Note that
the solution obtained by the source-removal algorithm is different from the one
obtained by the DFS-based algorithm. Both of them are correct, of course; the
topological sorting problem may have several alternative solutions.
The tiny
size of the example we used might create a wrong impression about the
topological sorting problem. But imagine a large project—e.g., in construction,
research, or software development—that involves a multitude of interrelated
tasks with known prerequisites. The first thing to do in such a situation is to
make sure that the set of given prerequisites is not contradictory. The
convenient way of doing this is to solve the topological sorting problem for
the project’s digraph. Only then can one start thinking about scheduling tasks
to, say, minimize the total completion time of the project. This would require,
of course, other algorithms that you can find in general books on operations
research or in special ones on CPM (Critical Path Method) and PERT (Program
Evaluation and Review Technique) methodologies.
As to
applications of topological sorting in computer science, they include
instruction scheduling in program compilation, cell evaluation ordering in
spread-sheet formulas, and resolving symbol dependencies in linkers.
Exercises
4.2
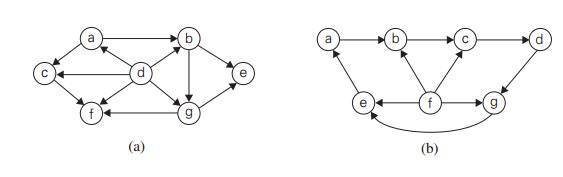
1. Apply the DFS-based algorithm to solve the topological sorting problem for the following digraphs:
2. a. Prove that the topological sorting problem has a solution if and only if it is a dag.
For a digraph with n
vertices, what is the largest number of distinct solutions the topological
sorting problem can have?
3. a. What is the time efficiency of the DFS-based algorithm for topological sorting?
b. How can one modify the DFS-based algorithm to avoid reversing the vertex ordering generated by DFS?
4. Can one use the order in which vertices are pushed onto the DFS stack (instead of the order they are popped off it) to solve the topological sorting problem?
5. Apply the source-removal algorithm to the digraphs of Problem 1 above.
6. a. Prove that a nonempty dag must have at least one source.
How would you find a source (or determine that such
a vertex does not exist) in a digraph represented by its adjacency matrix? What
is the time efficiency of this operation?
How would you find a source (or determine that such
a vertex does not exist) in a digraph represented by its adjacency lists? What
is the time efficiency of this operation?
7. Can you implement the source-removal algorithm for a digraph represented by its adjacency lists so that its running time is in O(|V | + |E|)?
8. Implement the two topological sorting algorithms in the language of your choice. Run an experiment to compare their running times.
9. A digraph
is called strongly connected if for any pair of two distinct vertices u and v there
exists a directed path from u to v and a directed path from v to u. In
general, a digraph’s vertices can be partitioned into disjoint maximal subsets
of vertices that are mutually accessible via directed paths; these subsets are
called strongly connected components of the digraph. There are two
DFS- based algorithms for identifying strongly connected components. Here is
the simpler (but somewhat less efficient) one of the two:
Step 1 Perform a DFS traversal of the
digraph given and number its vertices
in the order they become dead ends.
Step 2 Reverse the directions of all the
edges of the digraph.
Step 3 Perform a DFS traversal of the
new digraph by starting (and, if necessary,
restarting) the traversal at the highest numbered vertex among still unvisited
vertices.
The
strongly connected components are exactly the vertices of the DFS trees
obtained during the last traversal.
Apply
this algorithm to the following digraph to determine its strongly connected
components:
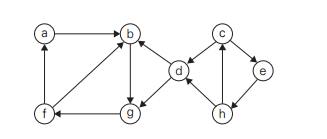
What is the time efficiency class of this
algorithm? Give separate answers for the adjacency matrix representation and
adjacency list representation of an input digraph.
How many strongly connected components does a dag
have?
10. Spider’s web A spider sits at the bottom (point S) of its web, and a fly sits at the top (F). How many different ways can the spider reach the fly by moving along the web’s lines in the directions indicated by the arrows? [Kor05]
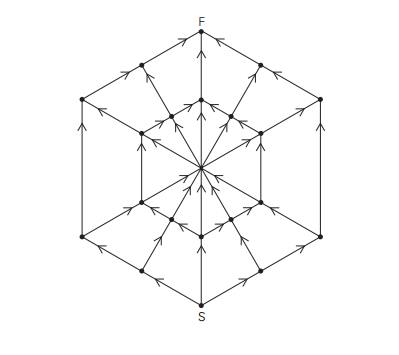
Related Topics