Cyclic codes, Error Control Coding

CYCLIC CODES:

In  coding theory, cyclic codes are  linear block error-correcting codes that have convenient algebraic structures for efficient  error detection and correction.

Let C be a linear code over a finite field GF(q)ⁿ of block length n. C is called a cyclic code, if for every codeword c=(c₁,...,c_n) from C, the word (c_n,c₁,...,c_n-1) in GF(q)ⁿ obtained by a cyclic right shift of components is again a codeword. Same goes for left shifts. One right shift is equal to n −1 left shifts and vice versa. Therefore the linear code C is cyclic precisely when it is invariant under all cyclic shifts.

Cyclic Codes have some additional structural constraint on the codes. They are based on Galois fields and because of their structural properties they are very useful for error controls. Their structure is strongly related to Galois fields because of which the encoding and decoding algorithms for cyclic codes are computationally efficient.

Cyclic code for correcting error:

a) For correcting single error

The cyclic codes explicitly with  error detection and correction. Cyclic codes can be used to correct errors, like  Hamming codes as a cyclic codes can be used for correcting single error. Likewise, they are also used to correct double errors and burst errors. All types of error corrections are covered briefly in the further subsections.

The Hamming code has a  generator polynomial g(x)=x³+x+1. This polynomial has a zero in  Galois extension field GF(8) at the primitive element a, and all codewords satisfy .

C(a)=0 Cyclic codes can also be used to correct double errors over the field GF(2). Blocklength will be n equal to 2^m-1 and primitive elements  a and a³ as zeros in the GF(2^m) because we are considering the case of two errors here, so each will represent one error.The received word is a polynomial of degree n-1 given as

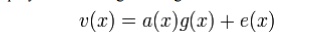
where e(x) can have at most two nonzero coefficients corresponding to 2 errors.

Syndrome Polynomial, S(x) as the remainder of polynomial v(x) when divided by the

generator polynomial g(x) i.e.

S(x)=v(x) mod g(x)= (a(x)g(x)+e(x)) mod g(x)=e(x) mod g(x) as (a(x)g(x)) mod g(x) is zero

b) For correcting two errors

Let the field elements X₁and X₂ be the two error location numbers. If only one error occurs then

X₂ is equal to zero and if none occurs both are zero.

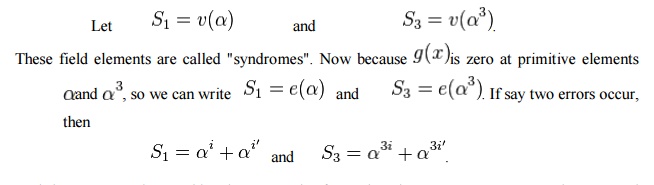
And these two can be considered as two pair of equations in GF(2m)  with two unknowns and

hence we can write

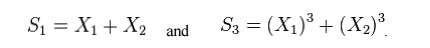
Hence if the two pair of nonlinear equations can be solved cyclic codes can used to correct two errors.

Syndrome Calculator

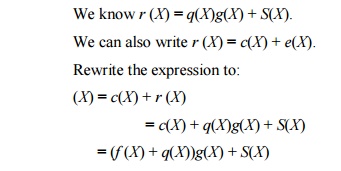
If error polynomial e(X) is divided by generator polynomial g(X), the remainder is the syndrome polynomial S(X).

Error Detection

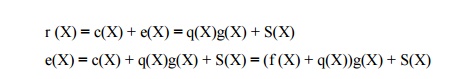
Investigate error detecting capability of cyclic code:

Assuming e(X) is a burst of length n - k or less, i.e., errors are confined to n - k or fewer consecutive positions;

e(X) can be expressed by e(X) = XjB(X), here B(X) is a polynomial of degree n –k –1 or less;

Xj cannot divided by g(X), B(X) cannot divided by g(X) neither, e(X) = X^jjB(X) is NOT divisible by g(X);

Thus the syndrome polynomial is not equal to zero.

It means that a cyclic code Ccyc (n,k) can detect any error burst of length n - k or less. A cyclic code Ccyc (n; k) can also detect all the end-around error bursts of length n - k or less.

e = (1 1 0 0 0 0 0 0 1 0 1)

Cyclic Redundancy Check (CRC) codes:

Cyclic redundancy .check codes are extremely well suited for "error detection". The two important reasons for this statement are,

(1) they can be designed to detect many combinations of likely errors.

(2) The implementation of both encoding and error detecting circuits is practical.

Accordingly, all error detecting codes used in practice, virtually, are of theCRC -type. In  ann-bit received word if a contiguous sequence of ‗b-bits‘ in which the first and the last bits and  any number of intermediate bits are received in error, then we say aCRC "error burst' of length has occurred. Such an error burst may also include an end-shifted version of the contiguous sequence.

In any event, Binary (n, k)CRC codes are capable of detecting the following error patterns:

1. All CRC error bursts of length (n-k) or less.

2. A fraction of (1 - 2 (n –k - 1)) of CRC error bursts of length (n – k + 1 ).

3. A fraction (1-2(n – k)) of CRC error bursts of length greater than (n – k + 1 ).

4. All combinations of (d min – 1 ) or fewer errors.

5. All error patterns with an odd number of errors if the generator polynomial g (X) has an even number of non zero coefficients.

Generator polynomials of three CRC codes, internationally accepted as standards are listed below.

All three contain (1 +X) as a prime factor. TheCRC-12 code is used when the character lengths is

6- bits. The others are used for 8-bit characters.

* CRC-12 code: g (X) = 1 + X + X²+X³+ X¹¹ + X¹²*

*CRC-16 code: g (X) = 1 +X²+ X¹⁵ + X¹⁶

*CRC-CCITT code: g (X) = 1 + X⁵+ x¹²+ X²⁶ .