Mutual Information

MUTUAL INFORMATION

On an average we require H(X) bits of information to specify one input symbol. However, if we are allowed to observe the output symbol produced by that input, we require, then, only H (X|Y) bits of information to specify the input symbol. Accordingly, we come to the conclusion, that on an average, observation of a single output provides with [H(X) –H (X|Y)]

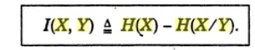
Notice that in spite of the variations in the source probabilities, p (x_k) (may be due to noise in the channel), certain probabilistic information regarding the state of the input is available, once the conditional probability p (x_k | y_j) is computed at the receiver end. The difference between the initial uncertainty of the source symbol x_k, i.e. log 1/p(x_k) and the final uncertainty about the same source symbol x_k, after receiving y_j, i.e. log1/p(x_k |y_j) is the information gained through the channel. This difference we call as the mutual information between the symbols x_k and y_j. Thus

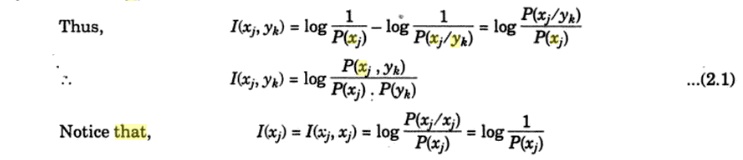
This is the definition with which we started our discussion on information theory. Accordingly I (x_k) is also referred to as ‘Self Information‘.

Eq (4.22) simply means that “the Mutual information ‟ is symmetrical with respect to its arguments.i.e.

I (x_k, y_j) = I (y_j, x_k)

Averaging Eq. (4.21b) over all admissible characters x_k and y_j, we obtain the average information gain of the receiver:

I(X, Y) = E {I (x_k, y_j)}

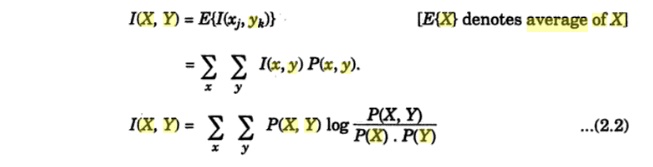
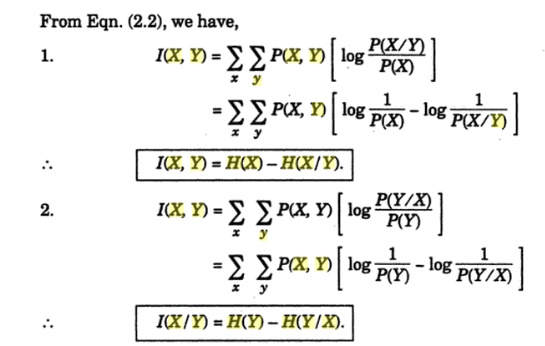
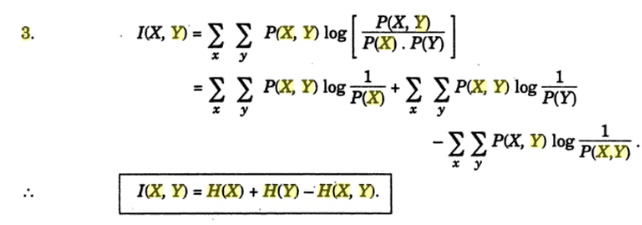
Or  I(X, Y) = H(X) + H(Y) –H(X, Y)

Further, we conclude that, ― even though for a particular received symbol, yj, H(X) –H(X | Yj) may be negative, when all the admissible output symbols are covered, the average mutual information is always non- negative‖. That is to say, we cannot loose information on an  average by observing the output of a channel. An easy method, of remembering the various relationships, is given in Fig 4.2.Althogh the diagram resembles a Venn-diagram, it is not, and the diagram is only a tool to remember the relationships. That is all. You cannot use this diagram for proving any result.

The entropy of X is represented by the circle on the left and that of Y by the circle on the right. The overlap between the two circles (dark gray) is the mutual information so that the remaining (light gray) portions of H(X) and H(Y) represent respective equivocations. Thus we have

H(X | Y) = H(X) –I(X, Y) and H (Y| X) = H(Y) –I(X, Y)

The joint entropy H(X,Y) is the sum of H(X) and H(Y) except for the fact that the overlap is added twice so that

H(X, Y) = H(X) + H(Y) - I(X, Y)

Also observe H(X, Y) = H(X) + H (Y|X)

= H(Y) + H(X |Y)

For the JPM given by I(X, Y) = 0.760751505 bits / sym