Chapter: Analog and Digital Communication
Entropy, Source Encoding Theorem
ENTROPY,
SOURCE ENCODING THEOREM
Source encoding theorem
The discrete memory less source of entropy H(X), the average code word length (L) for any distortion less source encoding is bounded.
Code redundancy is the
measure of redundancy bits in the encoded message sequence.
Mutual
information is the amount of information transferred when Xi is transmitted and
Yi is received. It is represented by I(Xi,Yi) .The average mutual information
is defined as the amount of source information gain per received symbol.
A
block code of length n and 2k code words is calleda linear (n, k) code if and
only if its 2k code words form a k-dimensional subspace of the vector space of
all the n-tuples over the field GF(2). The message occurring frequently can be
assigned short code words, whereas message which occur rarely are assigned long
code word, such coding is called variable length coding.
The
efficient representation of data generated by a discrete source is known as
source encoding. This device that performs this representation is called source
encoder.
The types of error
control method
Error detection and retransmission
Error detection and correction
Channel
capacity is defined as the maximum of the mutual information that may be
transmitted through the channel.
The needs for encoding
To improve the efficiency of communication
To improve the transmission quality.
The
entropy of a source is a measure of the average amount of information per
source symbol in a long message. Channel coding theorem is applied for discrete
memory less additive white gaussian noise channels.
The advantages of
Shannon fano coding
1. Reduced
bandwidth
2. Reduced
noise
3. It
can be used for error detection and correction.
The objectives of
cyclic codes :
Encoding
and syndrome calculations can be easily implemented by using simple shift
register with feedback connection It is possible to design codes having useful error
correction properties
Source Coding Theorem
The
source coding theorem shows that (in the limit, as the length of a
stream of independent and identically-distributed random variable (data tends
to infinity) it is impossible to compress the data such that the code rate
(average number of bits per symbol) is less than the Shannon entropy of the
source, without it being virtually certain that information will be lost.
However it is possible to get the code rate arbitrarily close to the Shannon
entropy, with negligible probability of loss.
Proof: Source coding
theorem
Given
X is an i.i.d. source, its
time series X1, ..., Xn is i.i.d. with
entropy H(X) in the discrete-valued case and differential entropy
in the continuous-valued case. The Source coding theorem states that for any ε>
0 for any rate larger than the entropy of the source, there is large enough n
and an encoder that takes n i.i.d. repetition of the source, X1:n,
and maps it to n(H(X) +ε) binary bits such that the
source symbols X1:n are recoverable from the
binary bits with probability at least 1- ε.
Proof of Achievability.
Fix
some ε> 0, and let
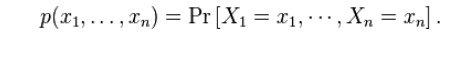
The typical set, Aεn,isdefined
as follows:

The
Asymptotic Equipartition Property (AEP) shows that for large enough n,
the probability that a sequence generated by the source lies in the typical
set, Aεn,as defined approaches one. In particular there for large enough
n,

The
encoding algorithm: The encoder checks if the input sequence lies within the
typical set; if yes, it outputs the index of the input sequence within the
typical set; if not, the encoder outputs an arbitrary n(H(X)
+ ε)digit number. As long as the input sequence lies within the typical
set (with probability at least 1- ε),the encoder doesn't make any error.
So, the probability of error of the encoder is bounded above by ε.
Proof of Converse. The
converse is proved by showing that any set of size smaller than Aε
n (in
the sense of exponent) would cover a set of probability bounded away from 1.
Proof: Source coding
theorem for symbol codes

where
the second line follows from Gibbs' inequality and the fifth line follows from
Kraft's inequality:
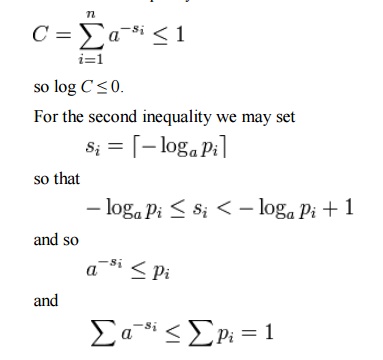
and so by Kraft's
inequality there exists a prefix-free code having those word lengths.
Thus the
minimal S
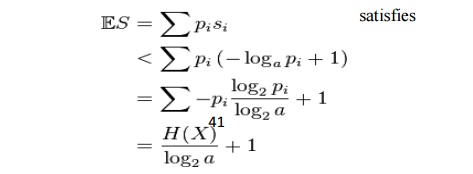
Related Topics