Channel Capacity theorem

Channel Capacity theorem

Shannon’s theorem:   on   channel   capacity(“coding Theorem”)

It is possible, in principle, to device a means where by a communication system will transmit information with an arbitrary small probability of error, provided that the information rate R(=r×I (X,Y),where r is the symbol rate) isC‘ calledlessthan―chao capacity‖.

The technique used to achieve this objective is called coding. To put the matter more formally, the theorem is split into two parts and we have the following statements.

Positive statement:

―Given a source of M equally likely messages, with M>>1, which is generating information at a rate R, and a channel with a capacity C. If R ≤C, then there exists a coding technique such that the output of the source may be transmitted with a probability of error of receiving the message that can be made arbitrarily small‖.

This theorem indicates that for R< C transmission may be accomplished without error even in the presence of noise. The situation is analogous to an electric circuit that comprises of only pure capacitors and pure inductors. In such a circuit there is no loss of energy at all as the reactors have the property of storing energy rather than dissipating.

Negative statement:

―Given the source of M equally likely messages with M>>1, which is generating information at a rate R and a channel with capacity C. Then, if R>C, then the probability of error of receiving the message is close to unity for every set of M transmitted symbols‖.

This theorem shows that if the information rate R exceeds a specified value C, the error probability will increase towards unity as M increases. Also, in general, increase in the complexity of the coding results in an increase in the probability of error. Notice that the situation is analogous to an electric network that is made up of pure resistors. In such a circuit,

whatever energy is supplied, it will be dissipated in the form of heat and thus is a ―lossy network‖.

You can interpret in this way: Information is poured in to your communication channel. You should receive this without any loss. Situation is similar to pouring water into a tumbler. Once the tumbler is full, further pouring results in an over flow. You cannot pour water more than your tumbler can hold. Over flow is the loss.

Shannon defines ― C‖ the channel capacity of a communication channel a s the maximum value of Transinformation, I(X, Y):

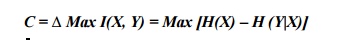
The maximization in Eq (4.28) is with respect to all possible sets of probabilities that could be    assigned   to   the   input   symbols.   Recall   the maximum power will be delivered to the load only when the load and the source are properly matched‘. The device used for this matching p in a radio receiver, for optimum response, the impedance of the loud speaker will be matched to the impedance of the output power amplifier, through an output transformer.

This theorem   is   also   known   as   ―The   Channel It may be stated in a different form as below:

There exists a coding scheme for which the source output can be transmitted over the channel and be reconstructed with an arbitrarily small probability of error. The parameter C/T_c is called the critical rate. When this condition is satisfied with the equality sign, the system is said to be signaling at the critical rate.

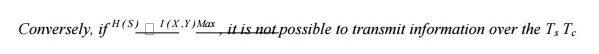
channel and reconstruct it with an arbitrarily small probability of error

A communication channel, is more frequently, described by specifying the source probabilities P(X) & the conditional probabilities P (Y|X) rather than specifying the JPM. The

CPM, P (Y|X), is usually referred tonoise characteristicasthe‘ ‗of the channel. unless otherwise specified, we shall understand that the description of the channel, by a matrix or        by   a   ‗Channel   diagram‘CPM,P(Y|X).Thus,alwaysindiscretecommunicationrefers   to channel with pre-specified noise characteristics (i.e. with a given transition probability matrix, P (Y|X)) the rate of information transmission depends on the source that drives the channel. Then, the maximum rate corresponds to a proper matching of the source and the channel. This ideal characterization of the source depends in turn on the transition probability characteristics of the given channel.

Bandwidth-Efficiency: Shannon Limit:

In practical channels, the noise power spectral density N₀ is generally constant. If E_b is the transmitted energy per bit, then we may express the average transmitted power as:

S = Eb C

(C/B) is the “bandwidth efficiency” of the syste m. If C/B = 1, then it follows that E_b = N₀. This  implies that the signal power equals the noise power. Suppose, B = B₀ for which, S = N, then Eq.  (5.59) can be modified as:

That is, "the maximum signaling rate for a given S is 1.443 bits/sec/Hz in the bandwidth  over which the signal power can be spread without its falling below the noise level”.