Critical Sections

CRITICAL SECTIONS

Matrix-vector multiplication was very easy to code because the shared-memory locations were accessed in a highly desirable way. After initialization, all of the variables—except y—are only read by the threads. That is, except for y, none of the shared variables are changed after they’ve been initialized by the main thread. Fur-thermore, although the threads do make changes to y, only one thread makes changes to any individual component, so there are no attempts by two (or more) threads to modify any single component. What happens if this isn’t the case? That is, what hap-pens when multiple threads update a single memory location? We also discuss this in Chapters 2 and 5, so if you’ve read one of these chapters, you already know the answer. But let’s look at an example.

Let’s try to estimate the value of . There are lots of different formulas we could use. One of the simplest is

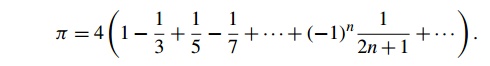
This isn’t the best formula for computing , because it takes a lot of terms on the right-hand side before it is very accurate. However, for our purposes, lots of terms will be better.

The following serial code uses this formula:

double factor = 1.0; 

double sum = 0.0;

for (i = 0; i < n; i++, factor = -factor) 

{ 

sum += -factor/(2* i+1);

}

pi = 4.0 sum;

We can try to parallelize this in the same way we parallelized the matrix-vector mul-tiplication program: divide up the iterations in the for loop among the threads and make sum a shared variable. To simplify the computations, let’s assume that the num-ber of threads, thread count or t, evenly divides the number of terms in the sum, n. Then, if n^ = n=t, thread 0 can add the first n^ terms. Therefore, for thread 0, the loop variable i will range from 0 to n^- 1. Thread 1 will add the next n^ terms, so for thread 1, the loop variable will range from n^ to 2n^- 1. More generally, for thread q the loop

Program 4.3: An attempt at a thread function for computing pi

          void  Thread_sum(void*  rank) {

          long my_rank = (long) rank;

          double factor;

          long long i;

          long long my_n    = n/thread count;

          long long     my first_i = my_n* my_rank;

          long long     my last_i = my first_i + my_n;

          if (my_first_i        % 2 ==        0)  /*  my first i is even  */

          factor = 1.0;

          else  /*  my_first_i is odd  */

          factor =  -1.0;

          for (i = my_first_i; i < my_last i; i++, factor =-    factor) {

          sum += factor/(2*i+1);

          }

          return NULL;

          }  /*  Thread sum  */

variable will range over

Furthermore, the sign of the first term, term qn^, will be positive if qn^ is even and negative if qnN is odd. The thread function might use the code shown in Program 4.3.

If we run the Pthreads program with two threads and n is relatively small, we find that the results of the Pthreads program are in agreement with the serial sum program. However, as n gets larger, we start getting some peculiar results. For example, with a dual-core processor we get the following results:

Notice that as we increase n, the estimate with one thread gets better and better. In fact, with each factor of 10 increase in n we get another correct digit. With n = 10⁵, the result as computed by a single thread has five correct digits. With n = 10⁶, it has six correct digits, and so on. The result computed by two threads agrees with the result computed by one thread when n = 10⁵. However, for larger values of n, the result computed by two threads actually gets worse. In fact, if we ran the program several times with two threads and the same value of n, we would see that the result computed by two threads changes from run to run. The answer to our original ques-tion must clearly be, “Yes, it matters if multiple threads try to update a single shared variable.”

Let’s recall why this is the case. Remember that the addition of two values is typically not a single machine instruction. For example, although we can add the contents of a memory location y to a memory location x with a single C statement,

x = x + y;

what the machine does is typically more complicated. The current values stored in x and y will, in general, be stored in the computer’s main memory, which has no circuitry for carrying out arithmetic operations. Before the addition can be carried out, the values stored in x and y may therefore have to be transferred from main memory to registers in the CPU. Once the values are in registers, the addition can be carried out. After the addition is completed, the result may have to be transferred from a register back to memory.

Suppose that we have two threads, and each computes a value that is stored in its private variable y. Also suppose that we want to add these private values together into a shared variable x that has been initialized to 0 by the main thread. Each thread will execute the following code:

y = Compute(my_rank); x = x + y;

Let’s also suppose that thread 0 computes y = 1 and thread 1 computes y = 2. The “correct” result should then be x = 3. Here’s one possible scenario:

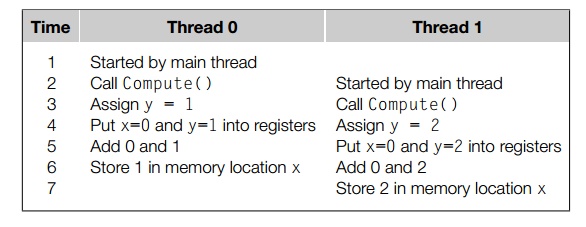
We see that if thread 1 copies x from memory to a register before thread 0 stores its result, the computation carried out by thread 0 will be overwritten by thread 1. The problem could be reversed: if thread 1 races ahead of thread 0, then its result may be overwritten by thread 0. In fact, unless one of the threads stores its result before the other thread starts reading x from memory, the “winner’s” result will be overwritten by the “loser.”

This example illustrates a fundamental problem in shared-memory programming: when multiple threads attempt to update a shared resource—in our case a shared variable—the result may be unpredictable. Recall that more generally, when multiple threads attempt to access a shared resource such as a shared variable or a shared file, at least one of the accesses is an update, and the accesses can result in an error, we have a race condition. In our example, in order for our code to produce the correct result, we need to make sure that once one of the threads starts executing the statement x = x + y, it finishes executing the statement before the other thread starts executing the statement. Therefore, the code x = x + y is a critical section, that is, it’s a block of code that updates a shared resource that can only be updated by one thread at a time.