Theorem with Solved Example Problems - CramerŌĆÖs Rule | 12th Business Maths and Statistics : Chapter 1 : Applications of Matrices and Determinants
Chapter: 12th Business Maths and Statistics : Chapter 1 : Applications of Matrices and Determinants
CramerŌĆÖs Rule
CramerŌĆÖs Rule
Gabriel Cramer, a Swiss mathematician born in the city Geneva in
31 July 1704. He edited the works of the two elder BernoulliŌĆÖs, and wrote on
the physical cause of the spheriodal shape of the planets and the motion of
their apsides (1730), and on NewtonŌĆÖs treatment of cubic curves (1746).
In 1750 he published CramerŌĆÖs Rule, giving a general formula for
the solution of certain linear system of n equations in n unknowns having a
unique solution in terms of determinants. Advantages of CramerŌĆÖs rule is that
we can find the value of x, y or z without knowing any of
the other values of x, y or z. CramerŌĆÖs rule is applicable
only when D ŌēĀ 0 ( is the determinant
value of the coefficient matrix) for unique solution.
Theorem (without proof) CramerŌĆÖs Rule:
Consider, 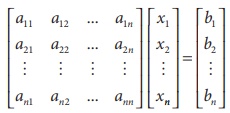
If AX = B is a system of n linear equations in ŌĆśnŌĆÖ unknowns such
that det (A) ŌēĀ 0, then the system has a unique solution.
This solution is,
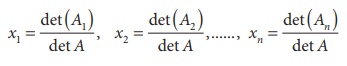
where Aj is the matrix obtained by replacing the
entries in the jth column of A by the entries in the
matrix

1. Non Homogeneous linear equations upto three variables.
(a) Consider the system of two linear equations with two unknowns.

The solution of unknown by CramerŌĆÖs rule is
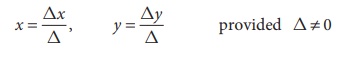
(b) Consider the system of three linear equations with three
unknowns a1
x + b1 y + c1 z = d1
a2 x + b2 y + c 2 z = d2
a3 x + b3 y + c 3 z = d3

Example 1.19
Solve the equations 2x + 3y = 7, 3x + 5y
= 9 by CramerŌĆÖs rule.
Solution:
The equations are
2x +
3y = 7
3x +
5y = 9
Here 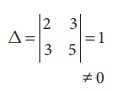
Ōł┤ we can apply CramerŌĆÖs
Rule
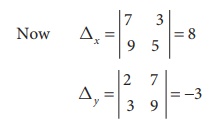
Ōł┤ By CramerŌĆÖs rule
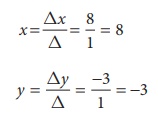
Ōł┤ Solution is x = 8, y = ŌłÆ3
Example 1.20
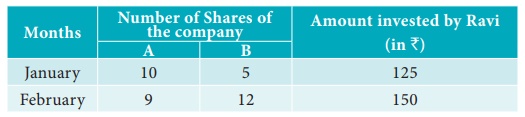
The following table represents the number of shares of two
companies A and B during the month of January and February and it
also gives the amount in rupees invested by Ravi during these two months for
the purchase of shares of two companies. Find the the price per share of A
and B purchased during both the months
Solution:
Let the price of one share of A be x
Let the price of one share of B be y
Ōł┤ By given data, we get
the following equations
10x +
5y = 125
9x +
12 y = 150
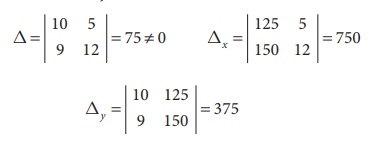
Ōł┤ By CramerŌĆÖs rule
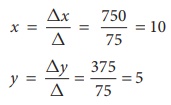
The price of the share A is Ōé╣10 and the price of the share B is Ōé╣5.
Example 1.21
The total cost of 11 pencils and 3 erasers is Ōé╣ 64 and the total
cost of 8 pencils and 3 erasers is Ōé╣49. Find the cost of each pencil and each
eraser by CramerŌĆÖs rule.
Solution:
Let ŌĆśxŌĆÖ be the cost of a pencil
Let ŌĆśyŌĆÖ be the cost of an eraser
Ōł┤ By given data, we get
the following equations
11x + 3y =64
8x+3y=49

Ōł┤ The cost of a pencil is Ōé╣ 5 and the cost of an eraser is Ōé╣ 3.
Example 1.22
Solve by CramerŌĆÖs rule x + y +
z = 4, 2x ŌłÆ y + 3z = 1, 3x + 2 y ŌłÆ z = 1
Solution:
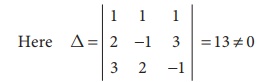
Ōł┤ We can apply CramerŌĆÖs
Rule and the system is consistent and it has unique solution.

The solution is ( x , y,
z) = ( ŌłÆ1,3, 2)
Example 1.23
The price of 3 Business Mathematics books, 2 Accountancy books and
one Commerce book is Ōé╣840. The price of 2 Business Mathematics books, one
Accountancy book and one Commerce book is Ōé╣570. The price of one Business
Mathematics book, one Accountancy book and 2 Commerce books is Ōé╣630. Find the
cost of each book by using CramerŌĆÖs rule.
Solution:
Let ŌĆśxŌĆÖ be the cost of a Business Mathematics book
Let ŌĆśyŌĆÖ be the cost of a Accountancy book.
Let ŌĆśzŌĆÖ be the cost of a Commerce book.
Ōł┤ 3x + 2 y + z = 840
2x +
y + z = 570
x + y + 2z = 630

Ōł┤ The cost of a Business
Mathematics book is Ōé╣120,
the cost of a Accountancy
book is Ōé╣150 and
the cost of a Commerce book is Ōé╣180.
Example 1.24
An automobile company uses three types of Steel S1,
S 2 and S3 for providing three different
types of Cars C1, C2 and C3.
Steel requirement R (in tonnes) for each type of car and total available
steel of all the three types are summarized in the following table.
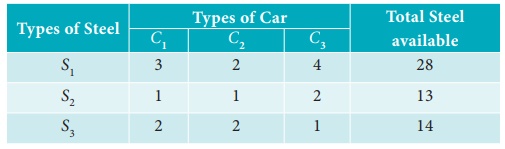
Determine the number of Cars of each type which can be produced by
CramerŌĆÖs rule.
Solution:
Let ŌĆśxŌĆÖ be the number of cars of type C1
Let ŌĆśyŌĆÖ be the number of cars of type C2
Let ŌĆśzŌĆÖ be the number of cars of type C3
3x +
2 y + 4z = 28
x + y + 2z = 13
2x +
2 y + z = 14

Ōł┤ The number of cars of
each type which can be produced are 2, 3 and 4.
Related Topics