Constants and Variables, Intervals and Neighbourhoods

Constants and Variables, Intervals and Neighbourhoods

To continue our discussion, we need certain prerequisites namely, constants, variables, independent variables, dependent variables, intervals and neighbourhoods.

1. Constants and Variables

A quantity that remains unaltered throughout a mathematical process is called a constant. A quantity that varies in a mathematical process is called a variable. A variable is an independent variable when it takes any arbitrary (independent) value not depending on any other variables, whereas if its value depends on other variables, then it is called a dependent variable.

We know the area A of a triangle is given by A = 1/2 bh. Here 1/2 is a constant and A, b, h are variables. Moreover b and h are independent variables and A is a dependent variable. We ought to note that the terms dependent and independent are relative terms. For example in the equation x + y = 1, x, y are variables and 1 is a constant. Which of x and y is dependent and which one is independent? If we consider x as an independent variable, then y becomes a dependent whereas if we consider y as an independent variable, then x becomes dependent.

Further consider the following examples:

i.            area of a rectangle A =  lb.

ii.            area of a circle A = πr².

iii.            volume of a cuboid V =  lbh.

From the above examples we can directly infer that b, h, l , r are independent variables; A and V are dependent variables and π is a constant .

2. Intervals and Neighbourhoods

The system R of real numbers can be represented by the points on a line and a point on the line can be related to a unique real number as in Figure 1.2. By this, we mean that any real number can be identified as a point on the line. With this identification we call the line as the real line.

The value increases as we go right and decreases as we go left. If x lies to the left of y on the real line then x < y. As there is no gap in a line, we have infinitely many real numbers between any two real numbers.

Note that the set of all natural numbers, the set of all non-negative integers, set of all odd integers, set of all even integers, set of all prime numbers are not intervals. Further observe that, between any two real numbers there are infinitely many real numbers and hence the above examples are not intervals.

Consider the following sets:

i.            The set of all real numbers greater than 0.

ii.            The set of all real numbers greater than 5 and less than 7.

iii.            The set of all real numbers x such that 1 ≤ x ≤ 3.

iv.            The set of all real numbers x such that 1 < x ≤ 2.

The above four sets are intervals. In particular (i) is an infinite interval and (ii), (iii) and (iv) are finite intervals. The term “finite interval” does not mean that the interval contains only finitely many real numbers, however both ends are finite numbers. Both finite and infinite intervals are infinite sets. The intervals correspond to line segments are finite intervals whereas the intervals that correspond to rays and the entire real line are infinite intervals.

A finite interval is said to be closed if it contains both of its end points and open if it contains neither of its end points. Symbolically the above four intervals can be written as (0, ∞), (5, 7), [1, 3], (1, 2]. Note that for symbolic form we used parentheses and square brackets to denote intervals. ( ) parentheses indicate open interval and [ ] square brackets indicate closed interval. The first two examples are open intervals, third one is a closed interval. Note that fourth example is neither open nor closed, that is, one end open and other end closed.

In particular [1, 3] contains both 1 and 3 and in between real numbers. The interval (1, 3) does not contain 1 and 3 but contains all in between the numbers. The interval (1, 2] does not contain 1 but contains 2 and all in between numbers.

Note that ∞ is not a number. The symbols −∞ and ∞ are used to indicate the ends of real line. Further, the intervals (a, b) and [a, b] are subsets of R.

Type of Intervals

There are many types of intervals. Let a, b ∈ R such that a < b. The following table describes various types of intervals. It is not possible to draw a line if a point is removed. So we use an unfilled circle “◦” to indicate that the point is removed and use a filled circle “•” to indicate that the point is included.

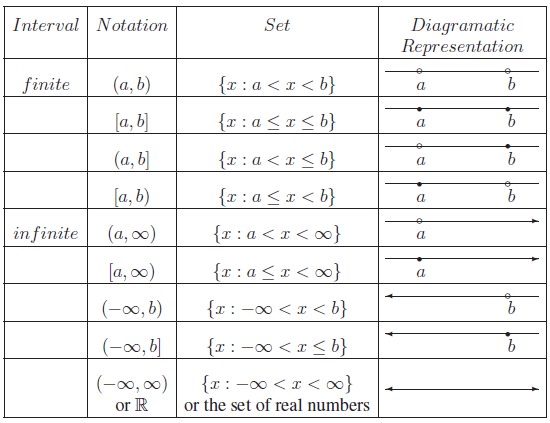
Try to write the following intervals in symbolic form.

Neighbourhood

Neighbourhood of a point ‘a’ is any open interval containing ‘a’. In particular, if Î is a positive number, usually very small, then the Î-neighbourhood of ‘a’ is the open interval (a − Î, a + Î). The set (a −Î , a +Î ) − {a} is called deleted neighbourhood of ‘a’ and it is denoted as 0 < |x − a| < Î (See Figure 1.3).