Chapter: 11th Mathematics : UNIT 12 : Introduction to Probability Theory
Classical definition (A priori) of probability (BernoulliŌĆÖs principle of equally likely)
Probability
Classical definition (A priori) of probability (BernoulliŌĆÖs principle of equally likely)
Earlier classes we have studied the frequency (A posteriori) definition of probability and the problems were solved. Now let us learn the fundamentals of the axiomatic approach to probability theory.
The basic assumption of underlying the classical theory is that the outcomes of a random experiment are equally likely. If there are n exhaustive, mutually exclusive and equally likely outcomes of an experiment and m of them are favorable to an event A, then the mathematical probability of A is defined as the ratio m/n . In other words, P ( A) = m/n .
Definition 12.13
Let S be the sample space associated with a random experiment and A be an event. Let n(S) and n(A) be the number of elements of S and A respectively. Then the probability of the event A is defined as

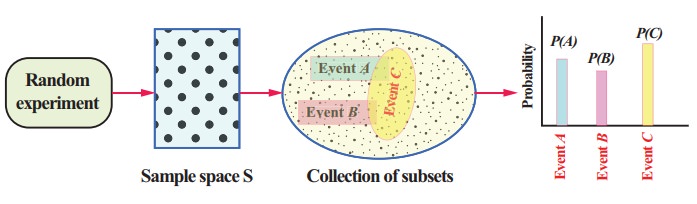
Every probabilistic model involves an underlying process is shown in the following figure.
The classical definition of probability is limited in its application only to situations where there are a finite number of possible outcomes. It mainly considered discrete events and its methods were mainly combinatorial. This renders it inapplicable to some important random experiments, such as ŌĆśtossing a coin until a head appearsŌĆÖ which give rise to the possibility of infinite set of outcomes. Another limitation of the classical definition was the condition that each possible outcome is ŌĆśequally likelyŌĆÖ.
These types of limitations in the classical definition of probability led to the evolution of the modern definition of probability which is based on the concept of sets. It is known an axiomatic approach.

The foundations of the Modern Probability theory were laid by Andrey Nikolayevich Kolmogorov, a Russian mathematician who combined the notion of sample space introduced by Richard von Mises, and measure theory and presented his axiomatic system for probability theory in 1933. We introduce the axiomatic approach proposed by A.N. Kolmogorov. Based on this, it is possible to construct a logically perfect structure of the modern theory of probability theory. The classical theory of probability is a particular case of axiomatic probability. The axioms are a set of rules, which can be used to prove theorems of probability.
Related Topics