Box plot

Box plot

A box plot can be used to graphically represent the data set. These plots involve five specific value.

(i) The lowest value of the data set (i.e., minimum), (ii) Q₁ (iii) The median (iv) Q₃ , (v) The highest value of the data set (i.e maximum)

These value are called a five-number summary of the data set.

A box plot is a graph of a data  set obtained by drawing a horizontal line from the minimum data value to Q₁ and a horizontal line from Q₃ to the maximum data value, and drawing a box by vertical lines passing through Q₁ and Q₃, with a vertical line inside the box passing through the median or Q₂.

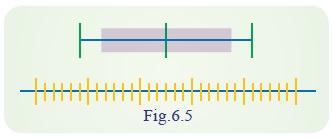
Description of boxplot

1.        If the median is near the center of the box, the distribution is approximately symmetric

2.        If the median falls to the left of the center of the box, the distribution is positively skewed.

3.        If the median falls to the right of the center of the box, the distribution is negatively skewed.

4.        If the lines are about the same length, the distribution is approximately symmetric

5.        If the right line is larger than the left line. the distribution is positively skewed.

6.        If the left line is larger than the right line. the distribution is negatively skewed.

Remark:

(i) The line drawn from minimum value of the dataset to Q1 and Q3 to the maximum value of the data set is called whisker.

(ii) Box plot is also called Box – Whisker plot.

(iii) A box and whisker plot illustrate the spread of the distribution and also gives an idea of the shape of the distribution

Example 6.20

The following data gives the Number of students studying in XI standard in 10 different schools 89,47,164,296,30,215,138,78,48,39 construct a boxplot for the data.

Solution:

Step 1 : Arrange the data in order

30,39,47,48,78,89,138,164,215,296

Step 2 : Find the median

Step 5 : Find the minimum and maximum values.

Step 6 : Locate the lowest value, Q₁, median, Q₃ and the highest value on the scale.

Step 7 : Draw a box through Q₁ and Q₃

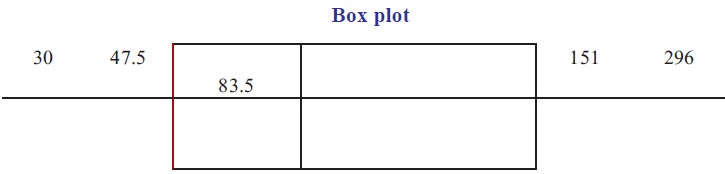
Example 6.21

Construct a box –whisker plot for the following data

96, 151, 167, 185, 200, 220, 246, 269, 238, 252, 297, 105, 123, 178, 202

Solution:

Step 1 : Arrange the data in code

96,105,123,151,167,178,185,200,202,220,238,246,252,269,297.

Step 2 : Find the Median

8th term Median = 200

Step 3 : Find Q₁ (middle of previous terms of 200)

96,105,123,151,167,178,185

Q₁ =151

Step 4 : Find Q₃ (middle of successive terms of 200)

202,220,238,246,252,269,297

Q₃ =246

Step 5 : Minimum value = 96, Maximum Value = 297

Step 6 : Draw a scale for the data on the x axis

Step 7: Locate the five numbers in the scale and draw a box around