Measures of Dispersion

Measures of Dispersion

Introduction

The measures of central tendency describes the central part of values in the data set appears to concentrate around a central value called average. But these measures do not reveal how these values are dispersed (spread or scattered) on each side of the central value. Therefore while describing data set it is equally important to know how for the item in the data are close around or scattered away from the measures of central tendency.

Example 6.1

Look at the runs scored by the two cricket players in a test match:

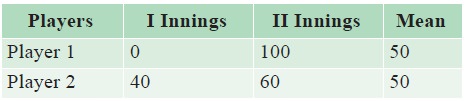
Comparing the averages of the two players we may come to the conclusion that they were playing alike. But player 1 scored 0 runs in I innings and 100 in II innings. Player 2 scored nearly equal runs in both the innings. Therefore it is necessary for us to understand data by measuring dispersion.