Relative Measures

Relative Measures

It is a pure number independent of the units of measurements. This measure is useful especially when the data sets are measured in different units of measurement.

For example, suppose a nutritionist would like to compare the obesity of school children in India and England. He collects data from some of the schools in these two countries. The weight is normally measured in kilograms in India and in pounds in England. It will be meaningless, if we compare the obesity of students using absolute measures. So it is sensible to compare them in relative measures.

Coefficient of Variation

The standard deviation is an absolute measure of dispersion. It is expressed in terms  of units in which the original figures are collected and stated. The standard deviation of heights of students cannot be compared with the standard deviation of weights of students, as both are expressed in different units, ie., heights in centimeter and weights in kilograms. Therefore the standard deviation must be converted into a relative measure of dispersion for the purpose of comparison. The relative measure is known as the coefficient of variation.

If we want to compare the variability of two or more series, we can use C.V. The series or groups of data for which the C.V is greater indicate that the group is more variable, less stable, less uniform, less consistent or less homogeneous. If the C.V is less, it indicates that the group is less variable, more stable, more uniform, more consistent or more homogeneous.

Merits:

The CV is independent of the unit in which the measurement has been taken, but standard deviation depends on units of measurement. Hence one should use the coefficient of variation instead of the standard deviation.

Limitations:

If the value of mean approaches 0, the coefficient of variation approaches infinity. So the minute changes in the mean will make major changes.

Example 6.12

If the coefficient of variation is 50 per cent and a standard deviation is 4, find the mean.

Solution:

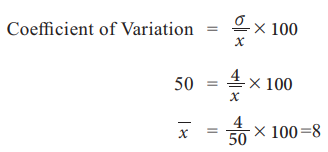
Example 6.13

The scores of two batsmen, A and B, in ten innings during a certain season, are as under:

Mean score = 50; Standard deviation = 5

Mean score = 75; Standard deviation = 25

Find which of the batsmen is more consistent in scoring.

Solution:

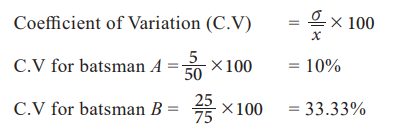
The batsman with the smaller C.V is more consistent.

Since for Cricketer A, the C.V is smaller, he is more consistent than B.

Example 6.14

The weekly sales of two products A and B were recorded as given below

Find out which of the two shows greater fluctuations in sales.

Solution:

For comparing the fluctuations in sales of two products, we will prefer to calculate coefficient of variation for both the products.

Product A: Let A=56 be the assumed mean of sales for product A.

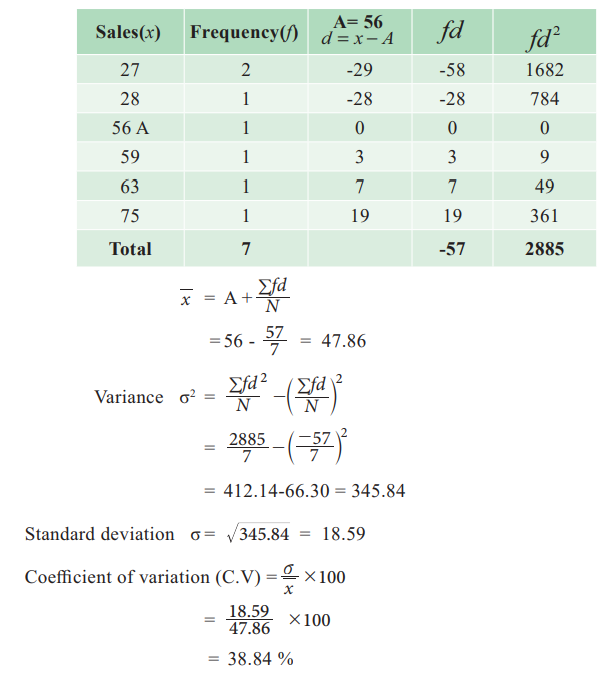
Product B: 

Since the coefficient of variation for product A is more than that of product B,

Therefore the fluctuation in sales of product A is higher than product B.