Standard Deviation

Standard Deviation

Consider the following data sets.

It is obvious that the range for the three sets of data is 8. But a careful look at these sets clearly shows the numbers are different and there is a necessity for a new measure  to address the real variations among the numbers in the three data sets. This variation is measured by standard deviation. The idea of standard deviation was given by Karl Pearson in 1893.

Definition

 ‘Standard deviation is the positive square root of average of the deviations of all the observation taken from the mean.’ It is denoted by a greek letter v.

a. Ungrouped data

x1 , x2 , x3  ... xn are the ungrouped data then standard deviation is calculated by

b. Grouped Data (Discrete)

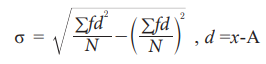
Where, f = frequency of each class interval

N = total number of observation (or elements) in the population

x = mid – value of each class interval

where A is an assumed A.M.

c. Grouped Data (continuous)

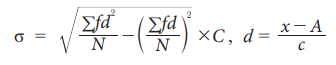
Where, f = frequency of each class interval

N = total number of observation (or elements) in the population

c = width of class interval

x = mid-value of each class interval where A is an assumed A.M.

Variance : Sum of the squares of the deviation from mean is known as Variance.

The square root of the variance is known as standard deviation. 

Example 6.5

The following data gives the number of books taken in a school library in 7 days find the standard deviation of the book taken

7, 9, 12, 15, 5, 4, 11

Solution:

Actual mean method

Merits:

·           The value of standard deviation is based on every observation in a set of data.

·           It is less affected by fluctuations of sampling.

·           It is the only measure of variation capable of algebraic treatment.

Limitations:

·           Compared to other measures of dispersion, calculations of standard deviation are difficult.

·           While calculating standard deviation, more weight is given to extreme values and less to those near mean.

·           It cannot be calculated in open intervals.

·           If two or more data set were given in different units, variation among those data set cannot be compared.

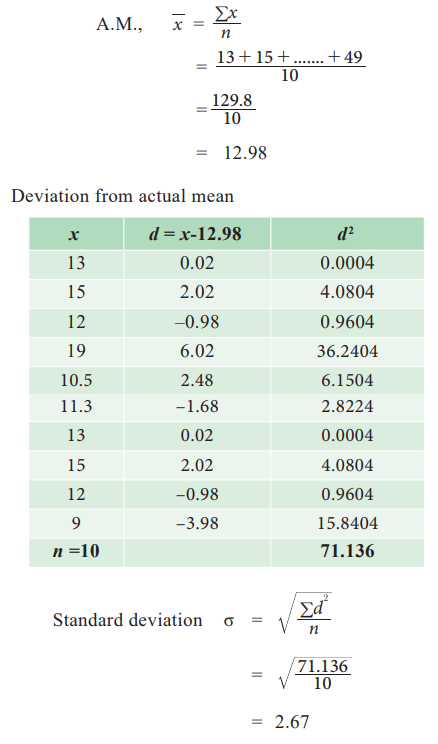
Example 6.6

Raw Data:

Weights of children admitted in a hospital is given below calculate the standard deviation of weights of children.

13, 15, 12, 19, 10.5, 11.3, 13, 15, 12, 9

Solution:

Example 6.7

Find the standard deviation of the first ‘n’ natural numbers.

Solution:

The first n natural numbers are 1, 2, 3,…, n. The sum and the sum of squares of these n numbers are

Example 6.8

The wholesale price of a commodity for seven consecutive days in a month is as follows:

Calculate the variance and standard deviation.

Solution:

The computations for variance and standard deviation is cumbersome when x values are large. So, another method is used, which will reduce the calculation time. Here we take the deviations from an assumed mean or arbitrary value A such that d = x – A

In this question, if we take deviation from an assumed A.M. =255. The calculations then for standard deviation will be as shown in below Table;

Example 6.9

The mean and standard deviation from 18 observations are 14 and 12 respectively. If an additional observation 8 is to be included, find the corrected mean and standard deviation.

Solution:

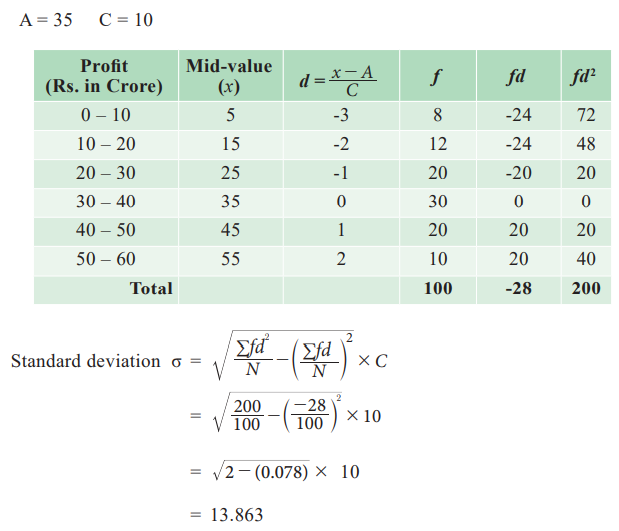
Example 6.10

A study of 100 engineering companies gives the following information

Calculate the standard of the profit earned.

Solution: