Fundamental Principles of counting

Fundamental Principles of counting

We use two fundamental principles of counting in solving the problems. They are addition rule on counting and multiplication rule on counting.

Fundamental Principle of addition on counting:

If an operation can be performed in m ways and if another operation can be performed in n ways and only one operation can be done at a time, then either of the two operations can be done at a time can be performed in m + n ways.

Example 7.1

In a box there are 5 red balls and 6 green balls. A person wants to select either a red ball or a green ball. In how many ways can the person make this selection?.

Solution:

Selection of a red ball from 5 balls in 5 ways.

Selection of a green ball from 6 balls in 6 ways.

By the fundamental Principle of addition, selection of a red ball or a green ball in (5+6) =11 ways.

Fundamental Principle of multiplication on counting:

If an operation can be performed in m ways and if another operation in n ways independent of the first, then the number of ways of performing both the operations simultaneously in m × n ways.

Example 7.2

A person has to travel from a place A to C through B. From A to B there are two routes and from B to C three routes. In how many ways can he travel from A to C?.

Solution:

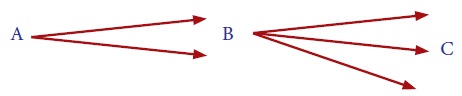
The person can travel from A to B in 2 ways and the person can travel from B to C in 3 ways.

By the Fundamental Principle of multiplication, the person can travel from A to C simultaneously in 2 × 3 = 6 ways.

[Note: Observe the answer part and the diagram carefully.]

Example 7.3

A company allots a code on each different product they sell. The code is made up of one English letter and two digit numbers. How many different codes are possible?

Solution:

There are 26 English Letters (A to Z) and other two digit numbers (0 to 9) are given.

The letter place can be filled in 26 ways with the 26 alphabets A to Z.

The ten’s place can be filled in 10 ways with the digits 0 to 9.

The unit’s place also can be filled in 10 ways with the digits 0 to 9.

So the number of product codes can be formed in 26 ×10 × 10 ways = 2600 ways.

Example 7.4

How many four digit numbers can be formed by using the digits 2, 5, 7, 8, 9, if the repetition of the digits is not allowed?.

Solution:

The thousand’s place can be filled with the 5 digits in 5 ways.

Since the repetition is not allowed, the hundred’s place can be filled with the remaining 4 ways.

Similarly, for the ten’s place can be filled with the remaining 3 digits in 3 ways and the unit’s place can be filled with the remaining 2 digits in 2 ways.

Therefore the number of numbers formed in 5 × 4 × 3 × 2 = 120 ways.

120 four digit numbers can be formed.

Factorial:

The consecutive product of first n natural numbers is known as factorial n and is denoted as n ! or ∟n

That is

 n! = n ×(n–1)× ...×3 ×2 × 1

 3! = 3 × 2 × 1

 4! = 4 × 3 × 2 × 1

 5! = 5 × 4 × 3 × 2 × 1

 6! = 6 × 5 × 4 × 3 ×2 × 1

 Also 6! = 6 × (5 × 4 × 3 × 2 × 1) = 6 × (5!)

 This can be algebraically expressed as n! = n (n – 1)!

 Note that 1! =1 and 0! = 1.