Chapter: 11th Statistics : Chapter 7 : Mathematical Methods
Introduction to Binomial, Exponential and Logarithmic series
Introduction
to Binomial, Exponential and Logarithmic series
Binomial series
A
binomial is an algebraic expression of two terms. Now let us see the following
binomial expansion and the number pattern we get adjacent to it.
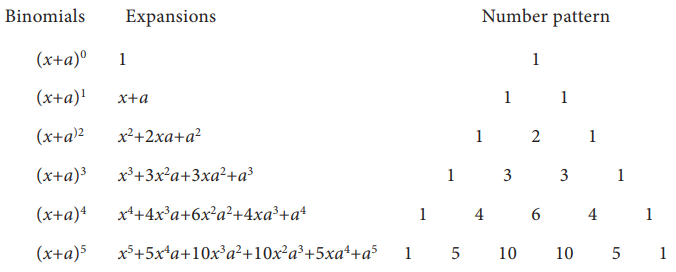
From
the above, we observe that the binomial coefficients form a number pattern
which is in a triangular form. This pattern is known as Pascal’s triangle. [ In
pascal’s triangle, the binomial coefficients appear as each entry is the sum of
the two above it.]
Binomial theorem for a positive integral index:
For
any natural number n
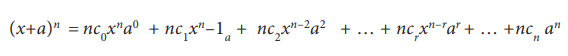
In
the above binomial expansion, we observe,
(i) The (r+1)th term is denoted by T r+1 = ncr xn–rar
(ii)
The degree of ‘x’ in each term decreases while
that of ‘a’ increases such that the sum of the power in each term
equal to n
(iii) nc0, nc1, nc2, … ncr, … ncn are binomial coefficients they are
also written as c0, c1, c2 … , cn
(iv)
From the relation ncr = ncn–r we see that the coefficients of
term equidistant from the beginning and the end are equal.
Example 7.15
Expand
(2x+y)5 using binomial theorem.
Solution:
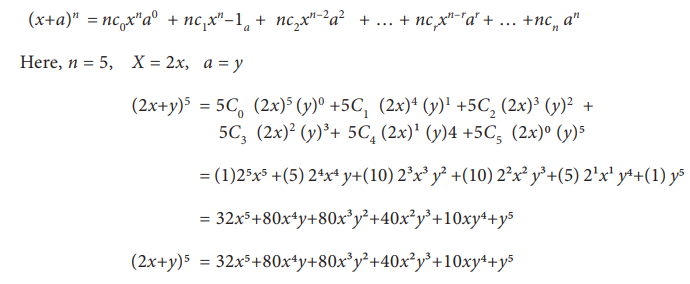
Example 7.16
Find
the middle terms of expansion (3x+y)5
Solution:
In
the expansion of (3x+y)5 we have totally 6 terms. From
this the middle terms are T3 and T4
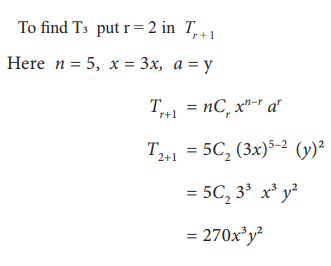
Similarly
we can find by putting r = 3 in Tr+1 to get T4 , then
T4 =90x2y3
Binomial theorem for a rational index:
For
any rational number other than positive integer
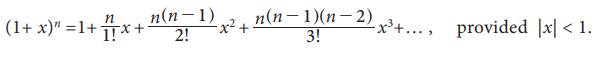
Some important expansions:
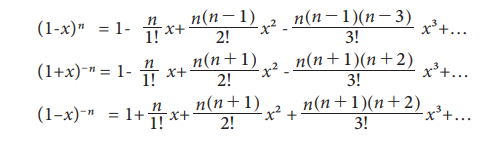
Special cases of infinite series:
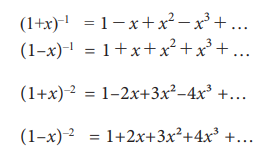
Example 7.17
Find the approximate value of 3√1002 (correct to 3 decimal places) using Binomial
series.
Solution:

Exponential series

Example 7.18

Solution:
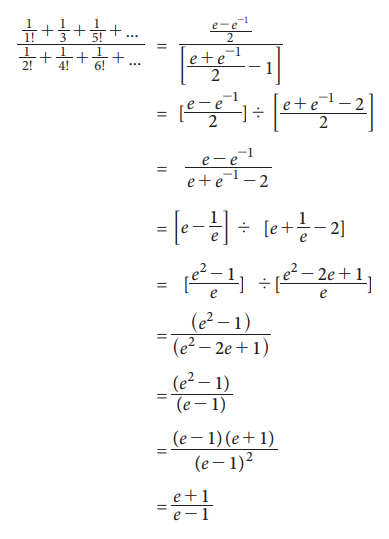
Logarithmic series:
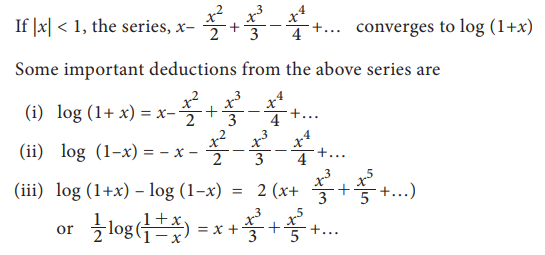
Related Topics