Mathematical Methods - Combinations | 11th Statistics : Chapter 7 : Mathematical Methods
Chapter: 11th Statistics : Chapter 7 : Mathematical Methods
Combinations
Combinations
Combination is a selection of objects without considering the
order of arrangements. For example out of three things A, B, C we have to
select two things at a time. This can be selected in three different ways as
follows.
AB
AC BC
Here the selection of object AB and BA are one and the same. The
order of arrangement is not considered in combination. Hence the number of
combinations from 3 different things taken 2 at a time is 3.
This is written symbolically 3C2 = 3.
Now we use the formula to find combination.
The number of combination of n different things, taken r at a
time is given by

Example 7.8
Find 10C3 and 8C4
Solution:
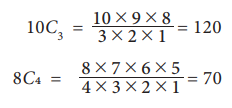
To
find 10 C 3 : In the numerator, first write the product of 3 natural
numbers starting from 10 in the descending order and in the denominator write
the factorial 3 and then simplify ].

Example 7.9
Out
of 13 players, 11 Players are to be selected for a cricket team. In how many
ways can this be done?
Solution:
Out
of 13 Players, 11 Players are selected in 13C11 ways

Example 7.10
In
how many ways a committee of 5 members can be selected from 6 men and 5 women,
consisting of 2 men and 3 women?
Solution:
For
a committee, 2 men and 3 women members are to be selected. From 6 men, 2 men
are selected in 6C2 ways. From 5 women, 3 women are selected in 5C3
ways.
Hence
a committee of 5 members (2 men and 3 women) is selected in
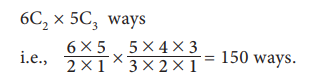
Example 7.11
How
many triangles can be formed by joining the vertices of a pentagon of five
sides.
Solution:
There
are 5 vertices in a pentagon. One triangle is formed by selecting a group of 3
vertices from given 5 vertices. This can be done in 5C3 ways.
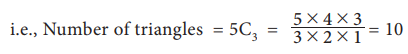
Example 7.12
A
question paper contains section A with 5 questions and section B with 7
questions.
A
student is required to attempt 8 questions in all, selecting at least 3 from
each section.
In
how many ways can a student select the questions?
Solution:
Selection
of 8 questions from 12 questions and at least 3 from each section is given
below.
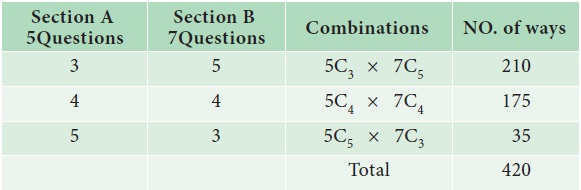
Therefore
total number of selection is 420
Example 7.13
If
6 Pr
= 360 and 6Cr = 15 find r.
Solution:
From the
formula,
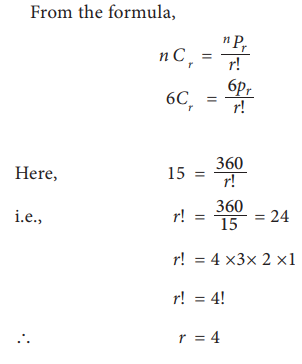
Example 7.14
If
nC8 = n C7, find n C15
Solution:
nC8
= n C7
nCn–8 = nC7
n–8 = 7
n = 15
Now, nC15 = 15C15 = 1.
Related Topics