Some rules, Important formulae, Solved Example Problems - Differentiation | 11th Statistics : Chapter 7 : Mathematical Methods
Chapter: 11th Statistics : Chapter 7 : Mathematical Methods
Differentiation
Differentiation
We Studied about functions and functional values in earlier classes. Functional value is an exact value. For some function f(x), when x = a, we obtain the functional value as f (a) = k.
Another type of approximation gives the very nearest value to the functional value is known as limiting value. So the limiting value is an approximate value. This limiting value approaches the nearest to the exact value k.
Suppose the exact value is 4, the limiting value may be 4.00000001 or 3.999999994. Here we observe that the functional value and the limiting value are more or less the same and there is no significant difference between them.
Hence in many occasions we use the limiting values for some critical problems.
The limiting value of f (x) when x approaches a number 2 is denoted by limx→2 f(x) = f(2) = l (some existing value)
The special type of any existing limit, 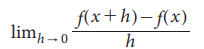 is called the derivative of the function f with respect to x and is denoted by f’ (x) . If y is a function of x, and has a derivative, then the differential coefficient of y with respect to x is denoted by dy/dx. This process of finding the limiting value is known as differentiation.
is called the derivative of the function f with respect to x and is denoted by f’ (x) . If y is a function of x, and has a derivative, then the differential coefficient of y with respect to x is denoted by dy/dx. This process of finding the limiting value is known as differentiation.
Some rules on differentiation:
(i) Derivative of a constant function is zero.
i.e., f´(c) = 0, where c is some constant.
(ii) If u is a function of x and k is some constant and dash denotes the differentiation,
[k u]´ = k[u]´
(iii) (u ± v)´ = u´ ± v´
(iv) (u v)´ = u´v + u v´ (product rule)
(v) 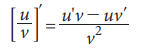 (quotient rule)
(quotient rule)
Important formulae:
( i) (xn) ´ = n xn-1
(ii) (ex)´ = ex
(iii) ( log x) ´ = 1/x
Example 7.19
Evaluate the following limits:
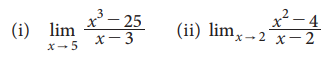
Solution:

Example 7.20
Find the derivative of the following with respect to x:
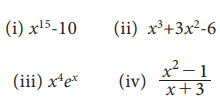
Solution:

Repeated differentiation:
If the derivative of a function is again differentiated with respect to the same variable, we say that the differentiation is the second order differentiation and is denoted as
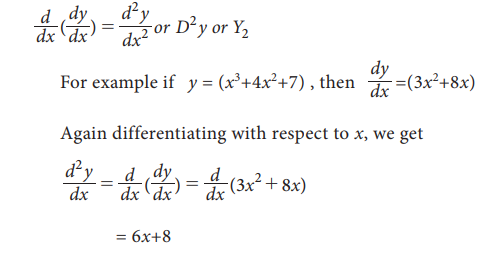
Related Topics