Permutations

Permutations

Permutation means arrangement of things in different ways. Let us take 3 things A, B, C for an arrangement. Out of these three things two at a time, we can arrange them in the following manner.

AB AC BC

BA CA CB

Here we find 6 arrangements. In these arrangements, order of arrangement is considered. Note that the arrangement AB and the arrangement BA are different.

The number of arrangements of the above is given as the number of permutation of 3 things taken 2 at a time which gives the value 6.

This is written symbolically 3P₂ = 6

Thus the number of arrangements that can be formed out of n things taken r at a time is known as the number of permutation of n things taken r at a time and is denoted as nP_r or P ( n, r)

We write nP_r as nP_r = n (n –1) ( n – 2) …. [n – (r–1)]

  The same nP_r can be written in factorial notation as follows:

To find 10 P₃, Start with 10, write the product of 3 consecutive natural numbers in the descending order]

Example 7.5

In how many ways can five students stand for a photograph in a row?

Solution:

The number of ways in which 5 students can stand in a row is same as the number of arrangements of 5 different things taken all at a time.

This can be done in 5P5 ways and 5P₅ = 5! = 120 ways.

Permutation of objects not all district:

The number of permutations of n objects, where p₁ objects are of one kind, p₂ are of second kind … p_k are of kth kind and the rest, if any, are of different kind is given by

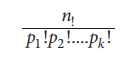
Example 7.6

Find the number of permutations of the letters in the word ‘STATISTICS’

Solution:

Here there are 10 objects (letters) of which there are 3S, 3 T, 2 I and 1A and 1C

Therefore the required number of arrangements is

Example 7.7

If 10 P_r = 720 find the value of r.

 10 P_r = 720

 10 P_r = 10 × 9 × 8

 10 P_r = 10 P₃

 r = 3