Basic LC Oscillator Tank Circuit

Basic LC Oscillator Tank Circuit

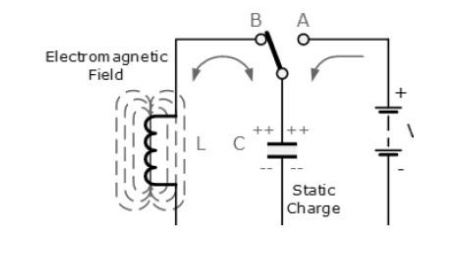
The circuit consists of an inductive coil, L and a capacitor, C. The capacitor stores energy in the form of an electrostatic field and which produces a potential (static voltage) across its plates, while the inductive coil stores its energy in the form of an electromagnetic field.

The capacitor is charged up to the DC supply voltage, V by putting the switch in position A. When the capacitor is fully charged the switch changes to position B. The charged capacitor is now connected in parallel across the inductive coil so the capacitor begins to discharge itself through the coil.

The voltage across C starts falling as the current through the coil begins to rise. This rising current sets up an electromagnetic field around the coil which resists this flow of current. When the capacitor, C is completely discharged the energy that was originally stored in the capacitor, C as an electrostatic filed is now stored in the inductive coil, L as an electromagnetic field around the coils windings.

As there is now no external voltage in the circuit to maintain the current within the coil, it starts to fall as the electromagnetic field begins to collapse. A back emf is induced in the coil (e= -Ldi/dt) keeping the current flowing in the original direction. This current now charges up the capacitor, c with the opposite polarity to its original charge.

C continues to chare up until the current reduces to zero and the electromagnetic field of the coil has collapsed completely. The energy originally introduced into the circuit through the switch, has been returned to the capacitor which again has an electrostatic voltage potential across it, although it is now of the opposite polarity. The capacitor now starts to discharge again back through the coil and the whole process os repeated. The polarity of the voltage changes as the energy is passed back and forth between the capacitor and inductor producing an AC type sinusoidal voltage and current waveform.

This then forms the basis of an LC oscillators tank circuit and theoretically this cycling back and forth will continue indefinitely. However, every time energy is transferred from C to L or from L to C losses occur which decay the oscillations.

This oscillatory action of passing energy back and forth between the capacitor, C to the inductor, L would continue indefinitely if it was not for energy losses within the circuit. Electrical energy is lost in the DC or real resistance of the inductors coil, in the dielectric of the capacitor, and in radiation from the circuit so the oscillation steadily decreases until they die away completely and the process stops.

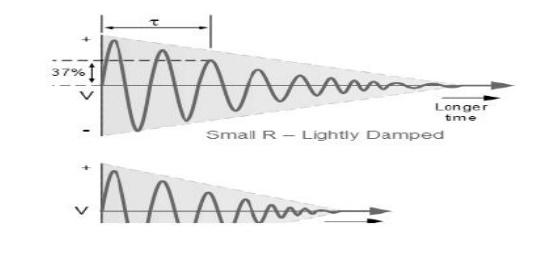
Then in a practical LC circuit the amplitude of the oscillatory voltage decreases at each half cycle of oscillation and will eventually die away to zero. The oscillations are then said to be "damped" with the amount of damping being determined by the quality or Q-factor of the circuit.

1. Damped Oscillations

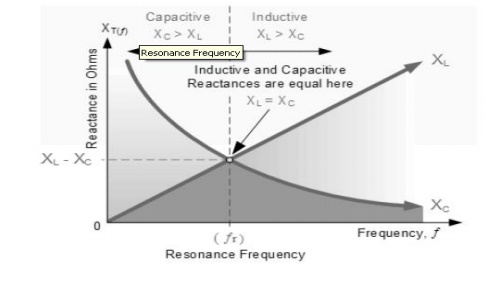
The frequency of the oscillatory voltage depends upon the value of the inductance and capacitance in the LC tank circuit. We now know that for resonance to occur in the tank circuit, there must be a frequency point were the value of X_C, the capacitive reactance is the same as the value of X_L, the inductive reactance (X_L = X_C) and which will therefore cancel out each other out leaving only the DC resistance in the circuit to oppose the flow of current.

If we now place the curve for inductive reactance on top of the curve for capacitive reactance so that both curves are on the same axes, the point of intersection will give us the resonance frequency point, ( ƒr or ωr ) as shown below.

2. Resonance Frequency

where: ƒ_r is in Hertz, L is in Henries and C is in Farads.

Then the frequency at which this will happen is given as:

Then by simplifying the above equation we get the final equation for  Resonant

Frequency, ƒr in a tuned LC circuit as:

3. Resonant Frequency of a LC Oscillator

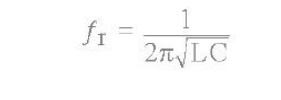
Where:

L is the Inductance in Henries

C is the Capacitance in Farads

ƒr is the Output Frequency in Hertz

This equation shows that if either L or C are decreased, the frequency increases. This output frequency is commonly given the abbreviation of ( ƒr ) to identify it as the "resonant frequency". To keep

the oscillations going in an LC tank circuit, we have to replace all the energy lost in each oscillation and also maintain the amplitude of these oscillations at a constant level.

The amount of energy replaced must therefore be equal to the energy lost during each cycle. If the energy replaced is too large the amplitude would increase until clipping of the supply rails occurs. Alternatively, if the amount of energy replaced is too small the amplitude would eventually decrease to zero over time and the oscillations would stop.

The simplest way of replacing this lost energy is to take part of the output from the LC tank circuit, amplify it and then feed it back into the LC circuit again. This process can be achieved using a voltage amplifier using an op-amp, FET or bipolar transistor as its active device.

However, if the loop gain of the feedback amplifier is too small, the desired oscillation decays to zero and if it is too large, the waveform becomes distorted. To produce a constant oscillation, the level of the energy fed back to the LC network must be accurately controlled.

Then there must be some form of automatic amplitude or gain control when the amplitude tries to vary from a reference voltage either up or down. To maintain a stable oscillation the overall gain of the circuit must be equal to one or unity. Any less and the oscillations will not start or die away to zero, any more the oscillations will occur but the amplitude will become clipped by the supply rails causing distortion. Consider the circuit below.