Answer the following questions

Computer Science: Algorithmic Problem Solving

Iteration and recursion

Evaluation

Answer the following questions

Part II

1. What is an invariant?

Answer: An expression involving variables, which remains unchanged by an assignment to one of these variables, is called an invariant of the assignment.

2. Define a loop invariant.

Answer: An invariant the loop body is known as a loop invariant. When the loop ends, the loop invariant has the same value.

3. Does testing the loop condition affect the loop invariant? Why?

Answer: Yes, it affects.

The loop invariants will be true on entry into a loop and following each iteration, so that on exit from the loop both the loop invariants and the loop termination condition can be guaranteed.

4. What is the relationship between loop invariant, loop condition and the input-output recursively

Answer:

(i) A loop invariant is a condition that is necessarily true immediately before and immediately after each iteration of a loop.

(ii) A loop invariant is some condition that holds for every iteration of the loop.

5. What is recursive problem solving?

Answer: Recursion step breaks the problem into sub-problems of smaller size, assumes solutions for sub-problems are given by recursive calls, and constructs solution to the given problem.

(Or)

Each solver should test the size of the input. If the size is small enough, the solver should output the solution to the problem directly. If the size is not small enough, the solver should reduce the size of the input and call a sub-solver to solve the problem with the reduced input.

6. Define factorial of a natural number recursively.

Answer: "The factorial of a number is the product of all the integers from 1 to that number."

factorial (n)

-- inputs : n is an integer, n ≥ o

-- outputs : factorial of n

 if n = 0 --base case

1

else

n * factorial (n − 1) -- recursion step.

Part III

1. There are 7 tumblers on a table, all standing upside down. You are allowed to turn any 2 tumblers simultaneously in one move. Is it possible to reach a situation when all the tumblers are right side up? (Hint: The parity of the number of upside down tumblers is invariant.)

Answer:

Tumbler problem

Since, the output needs to be to turn all tumblers up.

Let some variable u represent the number of tumblers that are upside down.

Model:

1. Two tumblers can be both upside up.

After turning u increments by 2.

2. Two tumblers are both upside down.

After turning u decrements by 2.

3. One is upside down and another is proper.

u is not changed.

So, after every step.

u is either incremented by 2 or decremented 2 or kept the same.

We can ignore the condition of u not being changed.

 Now, u := u+2

or

u := u − 2

The communicability (invariant) in this is that parity of u is not changing, i.e; if u is even at the beginning, its not changed at all and similarly if u is odd. That invariant is the initial state that needs to be defined. The final requirement is that u needs to become zero. This is possible only when the parity of u is zero i.e; u is even.

The final solution is if the number of tumblers that are upside down is even it is possible to get to a state by repeating the process for all the tumblers to be upside up.

2. A knockout tournament is a series of games. Two players compete in each game; the loser is knocked out (i.e. does not play any more), the winner carries on. The winner of the tournament is the player that is left after all other players have been knocked out. Suppose there are 1234 players in a tournament. How many games are played before the tournament winner is decided?

Answer:

Knockout tournament

12 3 4 initial number of players each round a player is laid off thus

n - number of remaining players,

r - total number of rounds,

k - number of rounds held assuming n is even

n,r: = n − k, r + k

n + r is invariant

winners is decided when n = 1

initially n + r = 1234, therefore r - 1233! (makes sense = 1233 rounds will eliminate 1233 players).

3. King Vikramaditya has two magic swords. With one, he can cut off 19 heads of a dragon, but after that the dragon grows 13 heads. With the other sword, he can cut off 7 heads, but 22 new heads grow. If all heads are cut off, the dragon dies. If the dragon has originally 1000 heads, can it ever die? (Hint:The number of heads mod 3 is invariant.)

Answer:

At first glance this problem is convoluted and intractable.

Once we hit upon the idea of using invariant, however it becomes trivial.

We note (13−19) = (22 − 7) = 0 (mod 3).

The magic swords can never change the number of heads of the dragon mod 3.

Since we start at 1000 =1 (mod 3). We can never get to 0. The dragons lives.

(or)

(i) If is 1000 heads.

(ii) You can now cut off 981 heads (multiple of 3) then cut the last 19 and the dragon will die.

(iii) The 13 heads won't come back after the dragon is killed. Unless it is a magic dragon.

Part IV

1. Assume an 8 × 8 chessboard with the usual coloring. "Recoloring" operation changes the color of all squares of a row or a column. You can recolor re-peatedly. The goal is to attain just one black square. Show that you cannot achieve the goal. (Hint: If a row or column has b black squares, it changes by (|8 - b) - b|).

Answer:

(i) We start with a normal colored chess board with number of black squares B=32 and number of white squares W=32.

(ii) So, W − B = 0 which is divisible by 4 and W+B = 64 W − B = 0 mod 4.

(iii) Whenever we change the colors of a row or column, we change the color of 8 squares.

(iv) Let this row (or column) have W white squares + B black squares W+B = 8. If this operation B increases by 2n, then W decreases by 2n so that W+B = 64. But B − W will change by 4n and if remain divisible by 4.

(v) W − B=0 mod 4.

(vi) After every operation “B-W mod 4” can have no other values.

(vii) But the required state has 63 white square and 1 black square, so it requires.

(viii) W − B = 63 − 1= 62 = 2 mod 4.

2. Power can also be defined recursively as

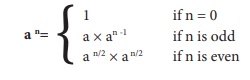
Construct a recursive algorithm using this definition. How many multiplications are needed to calculate a10?

Answer:

Power (a, n)

-- inputs n is an integer, n ≥ 0

-- outputs : aⁿ

if n = 0 -- base case

1

else

if (n%2! = 0) -- recursion step in case of odd

a × power (a, n − 1)

else

a × power (a, n/2) --recursion step in case of even.

3. A single-square-covered board is a board of 2n x 2n squares in which one square is covered with a single square tile. Show that it is possible to cover the this board with triominoes without overlap.

Answer: The size of the problem is n (board of size 2ⁿ × 2ⁿ). We can solve the problem by recursion. The base case is n = 1. It is a 2 × 2 corner-covered board. We can cover it with one triominoe and solve the problem. In the recursion step, divide the corner-covered board of size 2ⁿ × 2ⁿ into 4 sub-boards, each of size 2ⁿ − l × 2^n−l, by drawing horizontal and vertical lines through the centre of the board. Place a triominoe at the center of the entire board so as to not cover the corner-covered sub-board, as shown in the left-most board. Now, we have four corner- covered boards, each of size 2ⁿ⁻¹ × 2ⁿ⁻¹.

We have 4 sub-problems whose size is strictly smaller than the size of the given problem. We can solve each of the sub-problems recursively.

tile corner_covered board of size n

if n = 1 -- base case cover the 3 squares with one triominoe

else  --- recursion step divide board into 4 sub_boards of size n-1 place a triominoe at centre of board , leaving out the corner_covered sub -board tile each sub_board of size n-1

The resulting recursive process for covering a 2³ × 2³ corner-covered board is illustrated.