Choose the correct answer

Computer Science: Algorithmic Problem Solving

Iteration and recursion

Evaluation

Part I

1. A loop invariant need not be true

(a) at the start of the loop.

(b) at the start of each iteration

(c) at the end of each iteration

(d) at the start of the algorithm

2. We wish to cover a chessboard with dominoes, the number of black squares and the number of white squares covered by dominoes, respectively, placing a domino can bemodeled by

(a) b := b + 2

(b) w := w + 2

(c) b, w := b+1, w+1

(d) b := w

3. If m x a + n x b is an invariant for the assignment a, b : = a + 8, b + 7, the values of m and n are

(a) m = 8, n = 7

(b) m = 7, n = -8

(c) m = 7, n = 8

(d) m = 8, n = -7

Solution :

7a-8b

= 7(a+8) - 8 (b+7)

= 7a + 56 - 8b -56 = 7a - 8b.

4. Which of the following is not an invariant of the assignment? m, n := m+2, n+3

(a) m mod 2

(b) n mod 3

(c) 3 X m - 2 X n

(d) 2 X m - 3 X n

5. If Fibonacci number is defined recursively as

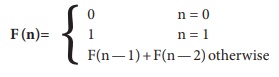
to evaluate F(4), how many times F() is applied?

(a) 3

(b) 4

(c) 8

(d) 9

6. Using this recursive definition

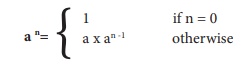
how many multiplications are needed to calculate a10?

(a) 11

(b) 10

(c) 9

(d) 8

Solution :

aⁿ = a × aⁿ -1

a¹⁰ = a × a⁹      (1)

=a × a × a⁸         (2)

= a × a × a × a⁷         (3)

= a × a × a × a × a⁶         (4)

 = a × a × a × a × a × a⁵         (5)

= a × a × a × a × a × a × a⁴         (6)

= a × a × a × a × a × a × a × a³         (7)

= a × a × a × a × a × a × a × a × a²         (8)

= a × a × a × a × a × a × a × a × a × a         (9)