Computer Science - Invariants - Examples | 11th Computer Science : Chapter 8 : Iteration and recursion
Chapter: 11th Computer Science : Chapter 8 : Iteration and recursion
Invariants - Examples
Invariants - Examples
The loop invariant is true in four
crucial points in a loop. Using the loop invariant, we can construct the loop
and reason about the properties of the variables at these points.
Example 8.5. Design an iterative algorithm to compute an. Let us name the
algorithm power(a, n). For example,
power(10, 4) = 10000
power (5 , 3) = 125
power (2 , 5) = 32
Algorithm power(a, n) computes an
by multiplying a cumulatively n times.
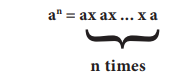
The specification and the loop
invariant are shown as comments.
power (a, n)
--inputs: n is a positive integer
outputs: p = an
p, i := 1 , 0
while i ≠ n
-- loop invariant: p = ai
p, i :=p X a, i+1
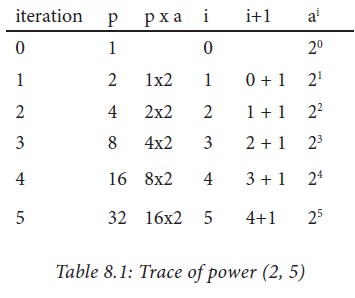
The step by step execution of
power (2, 5) is shown in Table 8.1. Each row shows the values of the two
variables p and i at the end of an iteration, and how they are calculated. We
see that p = ai is true at the start of the loop, and remains true
in each row. Therefore, it is a loop invariant.
When the loop ends, p = a1
is still true, but i = 5. Therefore, p = a5. In general, when the
loop ends, p = an. Thus, we have verified that power(a, n) satisfies
its specification.
Example 8.6. Recall the Chocolate bar problem of Example 1.11. How many
cuts are needed to break the bar into its individual squares?
We decided to represent the number
of pieces and the number of cuts by variables p and c respectively. Whenever a
cut is made, the number of cuts increases by one and the number of pieces also
increases by one. We decided to model it by an assignment.
p, c := p + 1, c+1
The process of cutting the bar can
be modeled by a loop. We start with one piece and zero cuts, p = 1 and c = 0.
Let n be the number of individual squares. When the number of pieces p equals
the number of individual squares n, the process ends.
p, c : = 1 , 0
while p ≠ n
p, c := p + 1, c+1
We have observed (in Example 8.2)
that p - c is an invariant of the assignment p, c := p + 1, c + 1. Let p - c =
k, where k is a constant. The points in the algorithm where p - c = k is true
are shown in the algorithm below, and in the flowchart of Figure 8.2.
p, c : = 1 , 0
1. -- p - c = k while p ≠ n
2. -- p - c = k
p, c := p+1, c+1
3. -- p - c = k
4. --p-c=k,p=n
The loop invariant p- c = k is
True at the start of the loop (line 1). Moreover, at the start of the loop, p-
c = 1. Therefore, k = 1, and the loop invariant is p - c = 1

When the loop ends (line 4), the
loop invariant is still true (p - c = 1). Moreover, the loop condition is false
(p = n). From p - c = 1 and p = n,
1.
p — c = 1 loop
invariant
2.
p = nend of the loop
3.
n — c = 1 from 1, 2
4.
c = n — 1 from 3
When the process ends, the number
of cuts is one less than the number of squares.
Example 8.7. There are 6 equally spaced trees and 6 sparrows sitting on these trees,one sparrow on each tree. If a sparrow flies from one tree to another, then at the same time, another sparrow flies from its tree to some other tree the same distance away, but in the opposite direction. Is it possible for all the sparrows to gather on one tree?
Let us index the trees from 1 to
6. The index of a sparrow is the index of the tree it is currently sitting on.
A pair of sparrows flying can be modeled as an iterative step of a loop. When a
sparrow at tree i flies to tree i + d, another sparrow at tree j flies to tree
j — d. Thus, after each iterative step, the sum S of the indices of the
sparrows remains invariant. Moreover, a loop invariant is true at the start and
at the end of the loop.
At the start of the loop, the
value of the invariant is
S = 1 + 2 + 3 + 4 + 5 + 6 = 21
When the loop ends, the loop
invariant has the same value. However, when the loop ends, if all the sparrows
were on the same tree, say k, then S = 6k.

It is not possible — 21 is not a
multiple of 6. The desired final values of the sparrow indices is not possible
with the loop invariant. Therefore, all the sparrows cannot gather on one tree.
Example 8.8. Consider the Chameleons of Chromeland of Example 6.3.
There are 13 red, 15 green, and 17 blue chameleons on Chromeland. When two
chameleons of different colors meet they both change their color to the third
one (for example, if a red and a green meet, both become blue). Is it possible
to arrange meetings that result in all chameleons displaying blue color?
Let r, g, and b be the numbers of
red, green and blue chameleons. We can model the meetings of two types as an
iterative process. A meeting changes (r, g, b) into (r-1, g-1, b+2) or (r-1,
g+2, b-1) or (r+2, g-1, b-1). Consider, for example, the meeting of a red and a
green chameleon.
r, g, b := r-1, g-1, b+2
The difference in the numbers of
any two types either do not change or changes by 3. This is an invariant.
r - 1 - (g - 1) = r - g
r - 1 - (b + 2) = (r - b) - 3
g - 1 - (b + 2) = (g - b) - 3
This is true for all three cases.
If any two types differ in number by a multiple of 3 at the start of the
iterative process, the difference can be reduced in steps of 3, to 0, when the
iterative process ends. However, at the start,
r - g = 13 - 15 = -2
g - b = 15 - 17 = -2
g - r = 17 - 13 =4
No two colors differ in number by
a multiple of 3. Therefore, all the chameleons cannot be changed to a single
color.
Example 8.9. Jar of marbles: You are given a jar full of two kinds of
marbles, white and black, and asked to play this game. Randomly select two
marbles from the jar. If they are the same color, throw them out, but put
another black marble in (you may assume that you have an endless supply of
spare marbles). If they are different colors, place the white one back into the
jar and throw the black one away. If you knew the original numbers of white and
black marbles, what is the color of the last marble in the jar?
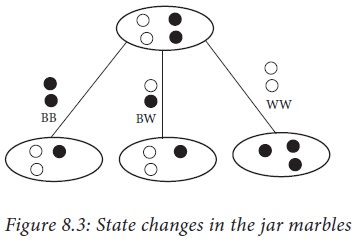
The number of white and black
marbles in the jar can be represented by two variables w and b. In each
iterative step, b and w change depending on the colors of the two marbles taken
out: Black Black, Black White or White White. It is illustrated in Figure 8.3
and annotated in the algorithm below.
1 while at least two marbles in
jar
2
-- b ,
w
3 take out any two marbles
4
case both are black -- BB
5throw away both the marbles
6put a black marble back
7 -- b = b '-1, w = w', b+w =
b'+w' -1
8 case both are white --WW
9 throw away both the marbles
10 put a black marble back
11--b = b'+1, w = w'-2, --b+w =
b'+w'-1
12
lse --BW
13 throw away the black one
14 put the white one back
15-- b = b'-1, w = w', b+w =
b'+w'-1
For each case, how b, w and b+w
change is shown in the algorithm, where b' and w' are values of the variables
before taking out two marbles. Notice the way w changes. Either it does not
change, or decreases by 2. This means that the parity of w, whether it is odd
or even, does not change. The parity of w is invariant.
Suppose, at the start of the game,
w is even. When the game ends, w is still even. Moreover, only one marble is
left, w+b = 1.
1 w + b = 1 end of the loop
2 w = 0orw = 1 from 1
3 w is even loop invariant
4 w = 0 from 2,3
5 b = 1 from 1,4
Last marble must be black.
Similarly, if at the start of the game, there is an odd number of whites, the
last marble must be white.
One last question: do we ever
reach a state with only one marble? Yes, because the total number of marbles
b+w always decreases by one at each step, it will eventually become 1.
Related Topics