Analog and Digital Data Conversions

Analog To Digital Conversion

The natural state of audio and video signals is analog. When digital technology was not yet around, they are recorded or played back in analog devices like vinyl discs and cassette tapes. The storage capacity of these devices is limited and doing multiple runs of re-recording and editing produced poor signal quality. Developments in digital technology like the CD, DVD, Blu-ray, flash devices and other memory devices addressed these problems.

For these devices to be used, the analog signals are first converted to digital signals using analog to digital conversion (ADC). For the recorded audio and video signals to be heard and viewed again, the reverse process of digital to analog conversion (DAC) is used.

ADC and DAC are also used in interfacing digital circuits to analog systems. Typical applications are control and monitoring of temperature, water level, pressure and other real-world data.

An ADC inputs an analog signal such as voltage or current and outputs a digital signal in the form of a binary number. A DAC, on the other hand, inputs the binary number and outputs the corresponding analog voltage or current signal.

Sampling rate

The analog signal is continuous in time and it is necessary to convert this to a flow of digital values. It is therefore required to define the rate at which new digital values are sampled from the analog signal. The rate of new values is called the sampling rate or sampling frequency of the converter.

A continuously varying band limited signal can be sampled (that is, the signal values at intervals of time T, the sampling time, are measured and stored) and then the original signal can be exactly reproduced from the discrete-time values by an interpolation formula. The accuracy is limited by quantization error. However, this faithful reproduction is only possible if the sampling rate is higher than twice the highest frequency of the signal. This is essentially what is embodied in the Shannon-Nyquist sampling theorem.

Since a practical ADC cannot make an instantaneous conversion, the input value must necessarily be held constant during the time that the converter performs a conversion (called the conversion time). An input circuit called a sample and hold performs this task—in most cases by using a capacitor to store the analog voltage at the input, and using an electronic switch or gate to disconnect the capacitor from the input. Many ADC integrated circuits include the sample and hold subsystem internally.

Accuracy

An ADC has several sources of errors. Quantization error and (assuming the ADC is intended to be linear) non-linearity is intrinsic to any analog-to-digital conversion. There is also a so-called aperture error which is due to a clock jitter and is revealed when digitizing a time-variant signal (not a constant value).

These errors are measured in a unit called the LSB, which is an abbreviation for least significant bit. In the above example of an eight-bit ADC, an error of one LSB is 1/256 of the full signal range, or about 0.4%.

Quantization error

Quantization error is due to the finite resolution of the ADC, and is an unavoidable imperfection in all types of ADC. The magnitude of the quantization error at the sampling instant is between zero and half of one LSB.

In the general case, the original signal is much larger than one LSB. When this happens, the quantization error is not correlated with the signal, and has a uniform distribution.

Its RMS value is the standard deviation of this distribution, given by  1/√12 LSB ≈ 0.289LSB. In the eight-bit ADC example, this represents 0.113% of the full signal range.

At lower levels the quantizing error becomes dependent of the input signal, resulting in distortion. This distortion is created after the anti-aliasing filter, and if these distortions are above 1/2 the sample rate they will alias back into the audio band. In order to make the Quantizing error independent of the input signal, noise with amplitude of 1 quantization step is added to the signal. This slightly reduces signal to noise ratio, but completely eliminates the distortion. It is known as dither.

Non-linearity

All ADCs suffer from non-linearity errors caused by their physical imperfections, resulting in their output to deviate from a linear function (or some other function, in the case of a deliberately non-linear ADC) of their input. These errors can sometimes be mitigated by calibration, or prevented by testing.

Important parameters for linearity are integral non-linearity (INL) and differential non- linearity (DNL). These non-linear ties reduce the dynamic range of the signals that can be digitized by the ADC, also reducing the effective resolution of the ADC.

D To A Converter- Specifications

D/A converters are available with wide range of specifications specified by manufacturer. Some of the important specifications are Resolution, Accuracy, linearity, monotonicity, conversion time, settling time and stability.

Resolution:

Resolution is defined as the number of different analog output voltage levels that can be provided by a DAC. Or alternatively resolution is defined as the ratio of a change in output voltage resulting for a change of 1 LSB at the digital input. Simply, resolution is the value of LSB.

Resolution (Volts) = VoFS  / (2ⁿ  - 1) = 1 LSB

increment Where ‘n’ is the number of input bits

‘VoFS’ is the full scale output voltage.

Example:

Resolution for an 8 – bit DAC for example is said to have

:     8 – bit resolution

:     A resolution of 0.392 of full-Scale (1/255)

:     A resolution of 1 part in 255.

Thus resolution can be defined in many different ways. 

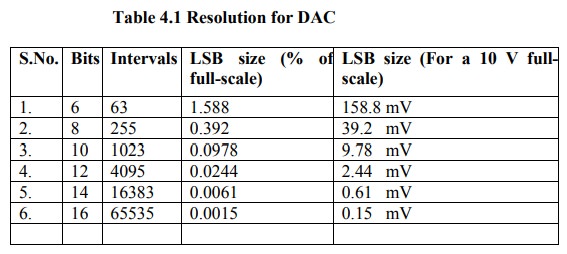
The following table shows the resolution for 6 to 16 bit DACs

Accuracy:

Absolute accuracy is the maximum deviation between the actual converter output and the ideal converter output. The ideal converter is the one which does not suffer from any problem. Whereas, the actual converter output deviates due to the drift in component values, mismatches, aging, noise and other sources of errors.

The relative accuracy is the maximum deviation after the gain and offset errors have been removed. Accuracy is also given in terms of LSB increments or percentage of full-scale voltage. Normally, the data sheet of a D/A converter specifies the relative accuracy rather than absolute accuracy.

Linearity:

Linearity error is the maximum deviation in step size from the ideal step size. Some D/A converters are having a linearity error as low as 0.001% of full scale. The linearity of a D/A converter is defined as the precision or exactness with which the digital input is converted into analog output. An ideal D/A converter produces equal increments or step sizes at output for every change in equal increments of binary input.

Monotonicity:

A Digital to Analog converter is said to be monotonic if the analog output increases for an increase in the digital input. A monotonic characteristic is essential in control applications. Otherwise it would lead to oscillations. If a DAC has to be monotonic, the error should be less than ± (1/2) LSB at each output level. Hence all the D/A converters are designed such that the linearity error satisfies the above condition.

When a D/A Converter doesn’t satisfy the condition described above, then, the output voltage may decrease for an increase in the binary input.

Conversion Time:

It is the time taken for the D/A converter to produce the analog output for the given binary input signal. It depends on the response time of switches and the output of the Amplifier. D/A converters speed can be defined by this parameter. It is also called as setting time.

Settling time: 

It is one of the important dynamic parameter. It represents the time it takes for the output to settle within a specified band ± (1/2) LSB of its final value following a code change at the input (Usually a full-scale change). It depends on the switching time of the logic circuitry due to internal parasitic capacitances and inductances. A typical settling time ranges from 100 ns to 10 µs depending on the word length and type of circuit used.

Stability:

The ability of a DAC to produce a stable output all the time is called as Stability. The performance of a converter changes with drift in temperature, aging and power supply variations. So all the parameters such as offset, gain, linearity error & monotonicity may change from the values specified in the datasheet. Temperature sensitivity defines the stability of a D/A converter.