Chapter: Civil : Principles of Solid Mechanics : Two Dimensional Solutions for Straight and Circular Beams
Airy’s Stress Function in Cartesian Coordinates
Airy’s Stress
Function in Cartesian Coordinates
To review once again, the basic field equations in
terms of stress are: Equilibrium:
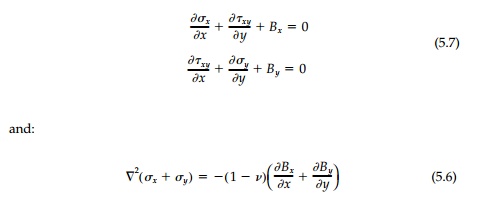
Once the stress field
is determined, the elastic strains and rotations are found from the
stressâ€'strain and conjugate relationships giving the components of the relative
deformation vector du, dv, dw which can then be integrated
for the displacement field.
In 1862, G.B. Airy introduced his potential function
defined as:

satisfied “by definition” and the compatibility
equation for plane stress becomes
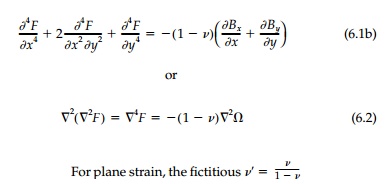
is substituted for v. If the body forces are given by a harmonic function (e.g.,
constant, linear, magnetic fields, seep-age, etc.), Equation (6.2) reduces to
the homogeneous elliptic form known as the biharmonic equation:

With this ingenious approach, Airy reduces the
two-dimensional prob-lem to solving one equation.* Generally, if body forces
are significant, their effect is solved for separately as in Chapter 5 and
introduced by superposi-tion. Therefore, unless specifically stated to be
otherwise, body forces will be neglected and Equation (6.3) used in this and
succeeding pages.
The Classic
Stress-Function Approach
Most solutions in two
dimensions, for other than linear stress fields where direct integration is
possible, can be obtained most easily by the semi-inverse method using stress
functions. Usually Airy’s stress function is employed which, in two dimensions,
reduces the three field equations to one fourth-order partial differential
equation.* This “biharmonic equation” is exact for plane strain and nearly so
for plane stress if the plate is reasonably thin.
Related Topics