Similar triangles

Similarity

Two figures are said to be similar if every aspect of one figure is proportional to other figure. For example: 

The above  houses  look  the  same  but different in size.  Both the mobile phones are the same but they vary in their sizes.  Therefore, mathematically we say that two objects are similar if they are of same shape but not necessarily they need to have the same size. The ratio of the corresponding measurements of two similar objects must be proportional.

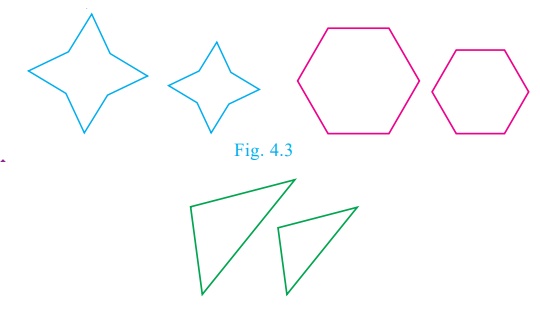
Here is a box of geometrical shapes. Collect the similar objects and list out.

In this chapter, we will be discussing specifically the use of similar triangles which is of utmost importance where if it is beyond our reach to physically measure the distance and height with simple measuring instruments. The concept of similarity is widely used in the fields of engineering, architecture and construction.

Here are few applications of similarity

(i) By analyzing the shadows that make triangles, we can determine the actual height of the objects.

(ii) Used in aerial photography to determine the distance from sky to a particular location on the ground.

(iii) Used in Architecture to aid in design of their work.

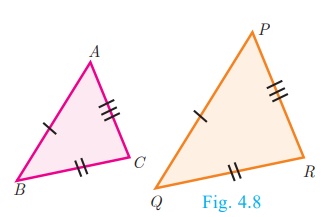
1. Similar triangles

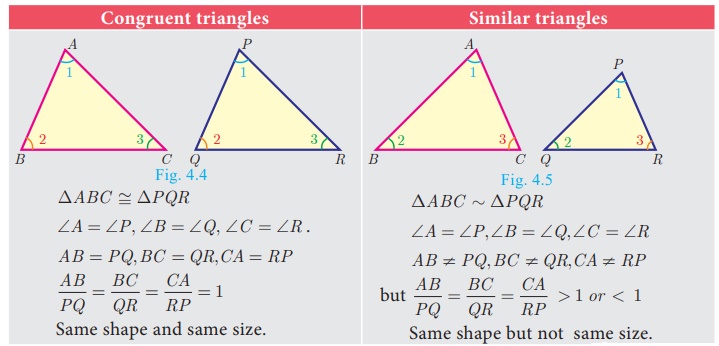
In class IX, we have studied congruent triangles. We can say that two geometrical figures are congruent, if they have same size and shape. But, here we shall study about geometrical figures which have same shape but proportional sizes. These figures are called “similar”.

Congruency and similarity of triangles

Congruency is a particular case of similarity. In both the cases, three angles of one triangle are equal to the three corresponding angles of the other triangle. _{DABC DPQR} But in congruent triangles, the corresponding sides are equal. While in similar triangles, the corresponding sides are proportional. 

Note

The traingles ABC and PQR are similar can be written as ΔABC ~ ΔPQR

2. Criteria of Similarity

The following criteria are sufficient to prove that two triangles are similar.

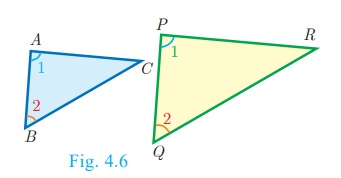
AA Criterion of similarity

If two angles of one triangle are respectively equal to two angles of another triangle, then the two triangles are similar, because the third angle in both triangles must be equal. Therefore, AA similarity criterion is same as the AAA similarity criterion.

So if ∠A = ∠P = 1 and ∠B = ∠Q = 2  then ΔABC ~ ΔPQR.

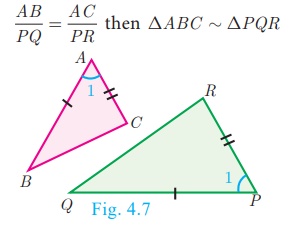
SAS Criterion of similarity

If one angle of a triangle is equal to one angle of another triangle and if the sides including them are proportional then the two triangles are similar.

Thus if ∠A = ∠P = 1 and 

AB/PQ = AC/PR then ΔABC ~ ΔPQR.

SSS Criterion of similarity

If three sides of a triangle are proportional to the three corresponding sides of another triangle, then the two triangles are similar.

So if, AB /PQ = AC /PR = BC /QR then ΔABC ~ ΔPQR

Thinking Corner: Are any two right angled triangles similar? If so why?

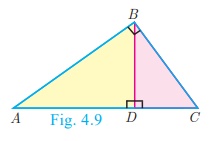
Some useful results on similar triangles

1. A perpendicular line drawn from the vertex of a right angled triangle divides the triangle into two triangles similar to each other and also to original triangle.

ΔADB ~ ΔBDC, ΔABC ~ ΔADB, ΔABC ~ ΔBDC

2. If two triangles are similar, then the ratio of the corresponding sides are equal to the ratio of their corresponding altitudes.

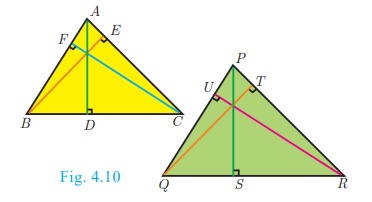
i.e. if ΔABC ~ ΔPQR then

AB/PQ = BC/QR = CA/RP = AD/PS = BE/QT = CF/RU

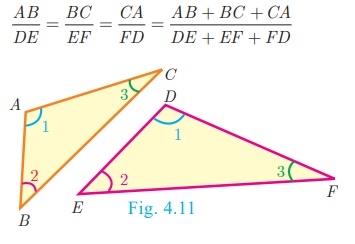
3. If two triangles are similar, then the ratio of C  the corresponding sides are equal to the ratio  of the corresponding perimeters.

ΔABC ~ ΔDEF then

AB/DE = BC/EF = CA/FD = [AB + BC +CA] / [DE + EF + FD]

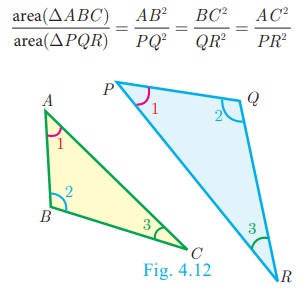
4. The ratio of the area of two similar triangles are equal to the ratio of the squares of their corresponding sides.

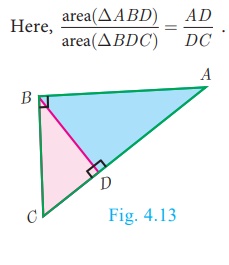
5. If two triangles have common vertex and their bases are on the same straight line, the ratio between their areas is equal to the ratio between the length of their bases.

Here, area( ABD) / area( BDC) = AD/DC

Definition 1

Two triangles are said to be similar if their corresponding sides are proportional.

Definition 2

The triangles are equiangular if the corresponding angles are equal.

Illustration

Two triangles, ΔXYZ and ΔLMN are similar because the corresponding angles are equal. 

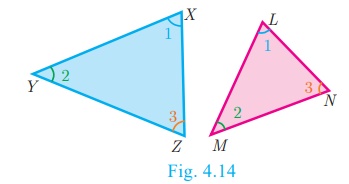
(i) ∠X = ∠L, ∠Y = ∠M,∠Z = ∠N (by angles)

(ii) XY/LM = YZ/MN = XZ/LN (by sides)

Here the vertices X, Y, Z correspond to the vertices L, M, N respectively. Thus in symbol ΔXYZ ~ ΔLMN

Note

(i) A pair of equiangular triangles are similar.

(ii) If two triangles are similar, then they are equiangular.

Example 4.1

Show that ΔPST ~ ΔPQR 

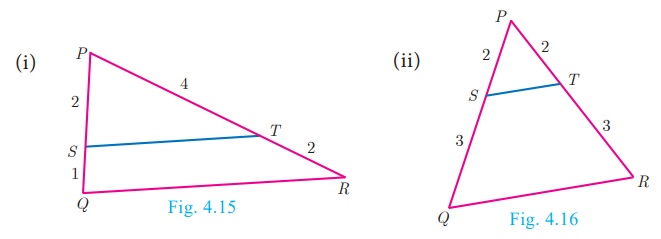
Solution

(i) In ΔPST and ΔPQR ,

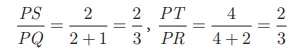
Thus, 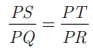 and ∠P is common

Therefore, by SAS similarity, ΔPST ~ ΔPQR

(ii) In ΔPST and ΔPQR ,

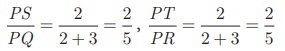
Thus, 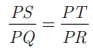 and ∠P is common

Therefore, by SAS similarity,

ΔPST ~ ΔPQR

Example 4.2

Is ΔABC ~ ΔPQR ?

Solution

In ΔABC and ΔPQR ,

The corresponding sides are not proportional. 

Therefore ΔABC is not similar to ΔPQR

Note

If we change exactly one of the four given lengths, then we can make these triangles similar.

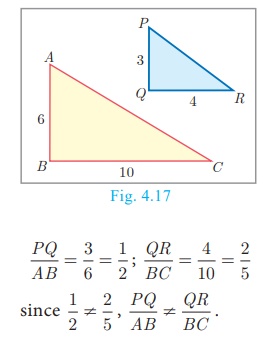
Example 4.3

Observe Fig.4.18 and find ∠P .

Solution

In ΔBAC and ΔPRQ , AB/RQ = 3/6 = 1/2;

Therefore, AB/RQ = BC/QP = PR/CA

By SSS similarity, we have Δ BAC ~ ΔQRP 

∠P = C (since the corresponding parts of similar triangle)

∠P = C = 180°− (∠A + ∠B) = 180° − (90° + 60°)

∠P = 180° − 150° = 30° 

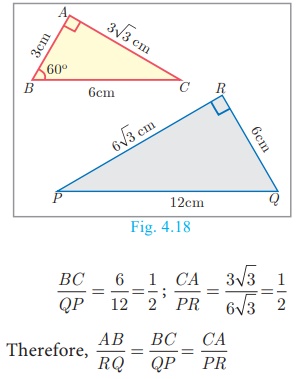
Example 4.4

A boy of height 90cm is walking away from the base of a lamp post at a speed of 1.2m/sec. If the lamppost is 3.6m A  above the ground, find the length of his shadow cast after 4 seconds.

Solution

Given, speed = 1.2 m/s,

time = 4 seconds

distance = speed × time = 1.2×4 = 4.8 m

Let x be the length of the shadow after 4 seconds 

Since, Δ ABE  ~ ΔCDE , 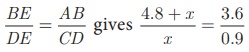  = 4  (since 90 cm = 0.9 m)

4.8 + x =4x gives 3x =4.8 so, x =1.6 m

The length of his shadow DE = 1.6 m

Example 4.5

In Fig.4.20 ∠A = ∠CED prove that ΔCAB ~  ΔCED. Also find the value of x.

Solution

In ΔCAB and ΔCED , ∠C is common, ∠A = CED

Therefore, ΔCAB ~ ΔCED (By AA similarity)

Example 4.6

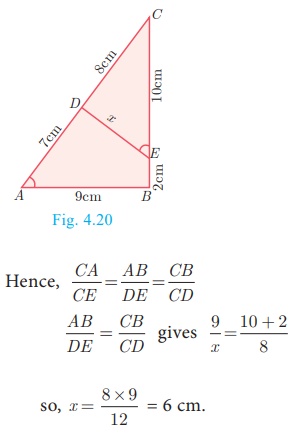
In Fig.4.21, QA and PB are perpendiculars to AB. If AO = 10 cm, BO= 6 cm and PB= 9 cm. Find AQ.

Solution

In ΔAOQ and ΔBOP , ∠OAQ = OBP = 90°

∠AOQ = BOP   (Vertically opposite angles)

Therefore, by AA Criterion of similarity, ΔAOQ ~ ΔBOP

Example 4.7

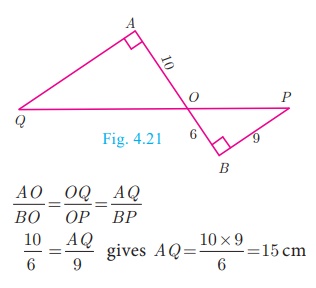
The perimeters of two similar triangles ABC respectively 36 cm and 24 cm. If PQ = 10 cm, find AB.

Solution

The ratio of the corresponding sides of similar triangles is same as the ratio of their perimeters. 

Since ΔABC ~ ΔPQR ,

Example 4.8

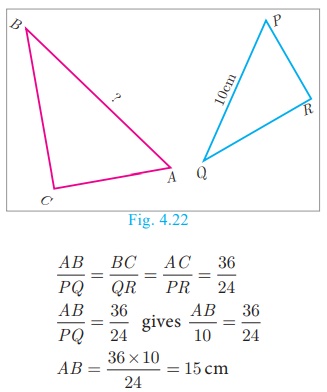
If ΔABC is similar to ΔDEF such that BC= 3 cm, EF= 4 cm and area of ΔABC = 54 cm². Find the area of ΔDEF .

Solution

Since the ratio of area of two similar triangles is equal to the ratio of the squares of any two corresponding sides, we have

Example 4.9

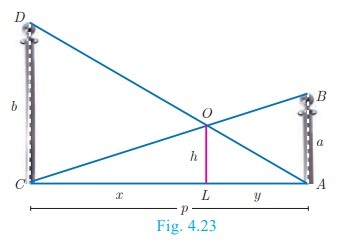
Two poles of height ‘a’ metres and ‘b’ metres are ‘p’ metres apart. Prove that the height of the point of intersection of the lines joining the top of each pole to the foot of the opposite pole is given by ab / a+b metres.

Solution

Let AB and CD be two poles of height ‘a’ metres and ‘b’ metres respectively such that the poles are ‘p’ metres apart. That is AC= p metres. Suppose the lines AD and BC meet at O, such that OL= h metres 

Let CL = x  and LA = y.

Then, x + y = p

In ΔABC and ΔLOC , we have

∠CAB = ∠CLO [each equal to 90° ]

∠C = ∠C [C is common]

ΔCAB ~ ΔCLO [By AA similarity]

In ΔALO and ΔACD , we have

∠ALO = ACD [each equal to 90° ]

∠A = ∠A [A is common]

Δ ALO ~ ΔACD [by AA similarity]

Therefore, h = ab / a+b  

Hence, the height of the intersection of the lines joining the top of each pole to the foot of the opposite pole is ab / a+b  metres.

3. Construction of similar triangles

So far we have discussed the theoretical approach of similar triangles and their properties. Now we shall discuss the geometrical construction of a triangle similar to a given triangle whose sides are in a given ratio with the corresponding sides of the given triangle.

This construction includes two different cases. In one, the triangle to be constructed is smaller and in the other it is larger than the given triangle. So, we use the following term called “scale factor” which measures the ratio of the sides of the triangle to be constructed with the corresponding sides of the given triangle. Let us take the following examples involving the two cases:

Example 4.10

Construct a triangle similar to a given triangle PQR with its sides equal to 3/5 of the corresponding sides of the triangle PQR (scale factor 3/5 < 1)

Solution

Given a triangle PQR we are required to construct another triangle whose sides are 3/5 of the corresponding sides of the triangle PQR.

Steps of construction

1. Construct a ΔPQR with any measurement.

2. Draw a ray QX making an acute angle with QR on the side opposite to vertex P.

3. Locate 5 (the greater of 3 and 5 in 3/5 ) points. 

Q₁, Q₂ ,Q ₃ ,Q₄  and Q₅  on QX so that QQ₁ = Q₁Q₂   = Q₂Q₃ = Q ₃Q₄   = Q ₄Q₅

4. Join Q₅ R and draw a line through Q₃  (the third point, 3 being smaller of 3 and 5 in 3/5 ) parallel to Q₅ R to intersect QR at R¢ .

5. Draw line through R’ parallel to the line RP to intersect QP at P’. 

Then, ΔP’QR is the required triangle each of whose sides is three-fifths of the corresponding sides of ΔPQR .

Example 4.11

Construct a triangle similar to a given triangle PQR with its sides equal to 7/4 of the corresponding sides of theP triangle PQR (scale factor 7/4 > 1)

Solution

Given a triangle PQR, we are required construct another triangle whose sides are 7/4 of the corresponding sides of the triangle PQR.

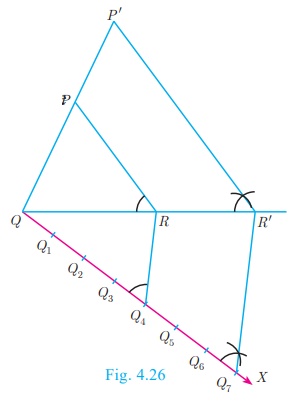
Steps of construction

1. Construct a ΔPQR with any measurement.

2. Draw a ray QX making an acute angle with QR on the side opposite to vertex P.

3. Locate 7 points (the greater of 7 and 4 in 7/4)

Q₁, Q₂ ,Q ₃ ,Q₄,Q₅,Q₆  and Q₇  on QX so that

QQ₁ = Q₁Q₂  = Q₂Q₃  = Q ₃Q₄  = Q ₄Q₅  = Q₅Q₆  = Q₆Q₇

4. Join Q₄ (the 4th point, 4 being smaller of 4 and 7 in 7/4 ) to R and draw a line through

Q₇ parallel to Q ₄ R, intersecting the extended line segment QR at R’.

5. Draw a line through R’ parallel to RP intersecting the extended line segment QP at P’.

Then ΔP′QR′ is the required triangle each of whose sides is seven-fourths of the corresponding sides of ΔPQR .