Chapter: Satellite Communication : Satellite Orbits
Look Angle Determination
Look Angle
Determination:
The
look angles for the ground station antenna are Azimuth and Elevation angles.
They are required at the antenna so that it points directly at the satellite.
Look angles are calculated by considering the elliptical orbit. These angles
change in order to track the satellite.
For
geostationary orbit, these angels values does not change as the satellites are
stationary with respect to earth. Thus large earth stations are used for
commercial communications.
For
home antennas, antenna beamwidth is quite broad and hence no tracking is
essential. This leads to a fixed position for these antennas.
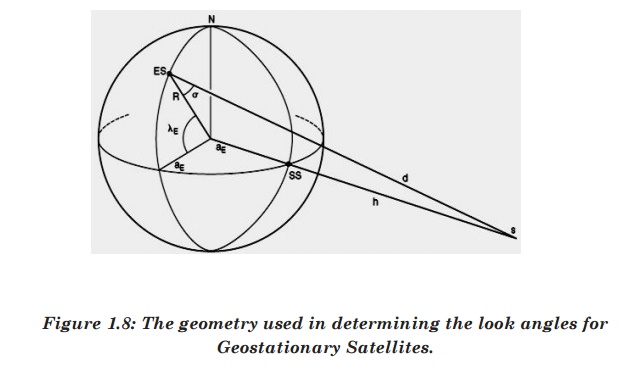
With
respect to the figure 1.8 and 1.9, the following information is needed to
determine the look angles of geostationary orbit.
1.
Earth Station Latitude: λE
2.
Earth Station Longitude: ΦE
3.
Sub-Satellite Point‟s Longitude: ΦSS
4.
ES: Position of Earth Station
5.
SS: Sub-Satellite Point
6.
S: Satellite
7.
d: Range from ES to S
8.
ζ: angle to be determined
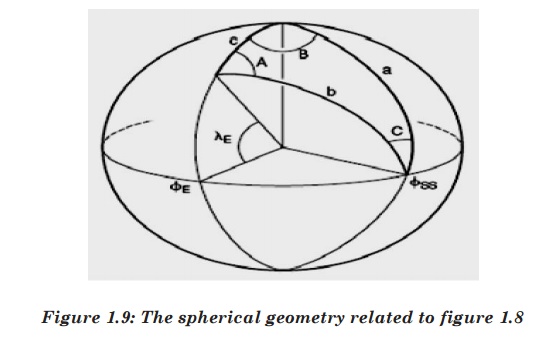
Considering
figure 3.3, it‟s a spherical triangle. All sides are the arcs of a great
circle. Three sides of this triangle are defined by the angles subtended by the
centre of the earth.
o
Side a: angle between North Pole and radius of the sub-satellite point.
o
Side b: angle between radius of Earth and radius of the sub-satellite point.
o
Side c: angle between radius of Earth and the North Pole.
a
=900 and such a spherical triangle is called quadrantal triangle. c
= 900 – λ
Angle
B is the angle between the plane containing c and the plane containing a.
Thus,
B = ΦE-ΦSS
Angle
A is the angle between the plane containing b and the plane containing c.
Angle
C is the angle between the plane containing a and the plane containing b.
Thus,
a = 900
c
= 900 - λE
B
= ΦE-ΦSS
Thus,
b = arcos (cos B cos λE)
And
A = arcsin (sin |B| / sin b)
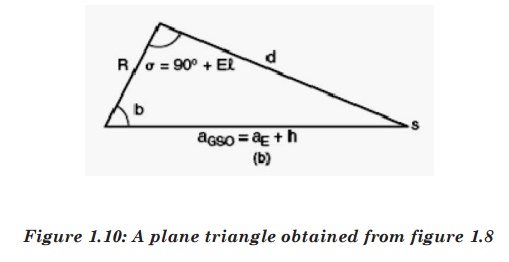
Applying
the cosine rule for plane triangle to the triangle of figure
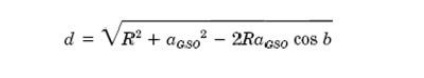
Applying
the sine rule for plane triangles to the triangle of figure 3.3 allows the
angle of elevation to be found:
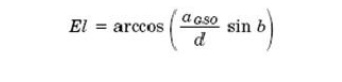
Related Topics