Exercise: Geometry

Unit Exercise

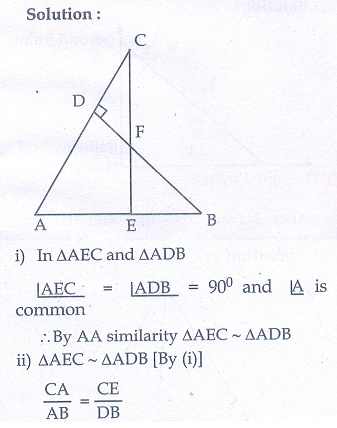
1. In the figure, if BD ┴ AC and CE ┴ AB , prove that

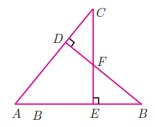
(i) ΔAEC  ~ ΔADB

(ii) CA/AB = CE/DB

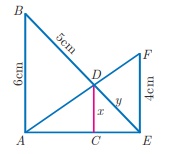
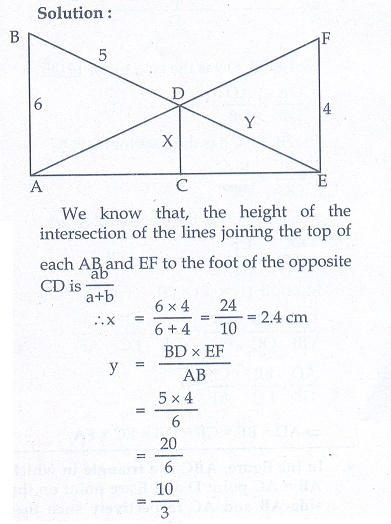
2. In the given figure AB || CD || EF .

If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.

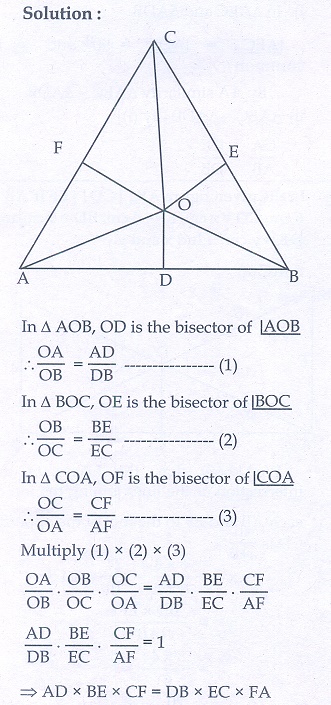
3. O is any point inside a triangle ABC. The bisector of ∠AOB , ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively. Show that AD × BE ×CF = DB ×EC ×FA

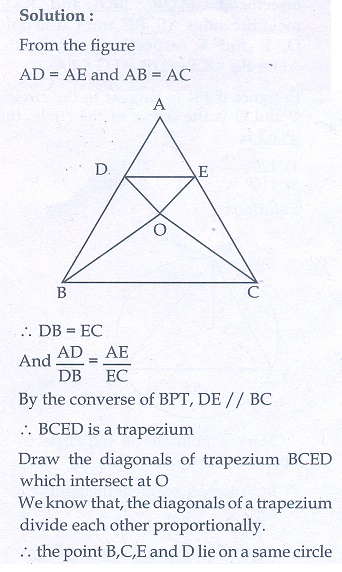
4. In the figure, ABC is a triangle in which AB = AC . Points D and E   D are points on the side AB and AC respectively such that AD = AE . Show that the points B, C, E and D lie on a same circle.

5. Two trains leave a railway station at the same time. The first train travels due west and the second train due north. The first train travels at a speed of 20 km/hr and the second train travels at 30 km/hr. After 2 hours, what is the distance between them?

6. D is the mid point of side BC and AE ┴ BC. If BC = a , AC = b , AB = c , ED = x , AD = p and AE = h , prove that

(i) b2  = p2 +ax + a2/4

(ii) c2  = p2 −ax + a2/4

(iii) b2 + c 2  = 2p2 + a2/2

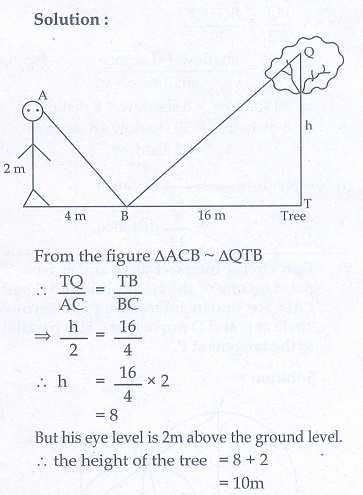
7. A man whose eye-level is 2 m above the ground wishes to find the height of a tree. e places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from the mirror B, he can see the reflection of the top of the tree. How height is the tree?

8. An emu which is 8 ft tall is standing at the foot of a pillar which is 30 ft high. It walks away from the pillar. The shadow of the emu falls beyond emu. What is the relation between the length of the shadow and the distance from the emu to the pillar?

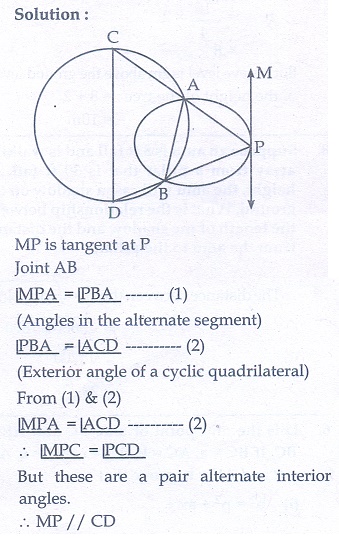
9. Two circles intersect at A and B. From a point P on one of the circles lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.

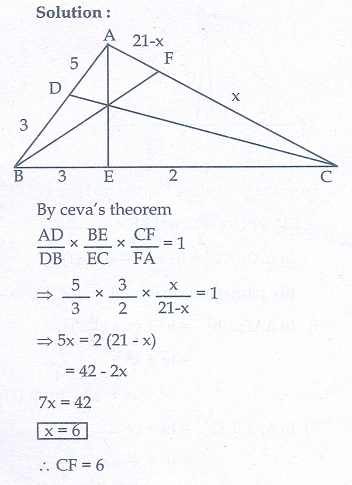
10. Let ABC be a triangle and D,E,F are points on the respective sides AB, BC, AC (or their extensions). Let AD : DB = 5 : 3 , BE : EC = 3 : 2 andAC = 21 . Find the length of the line segment CF.

Answer:

2. 12/5 cm, 10/3 cm

5. 20√13 km

7. 10 m

8. shadow = 4×11 (distance)

10. 14 units