Chapter: 12th Business Maths and Statistics : Chapter 1 : Applications of Matrices and Determinants
Echelon form and finding the rank of the matrix (upto the order of 3Ă4)
Echelon form and finding the rank of the
matrix (upto the order of 3Ă4)
A matrix A of order m Ă n is said to be in echelon form if
(i) Every row of A which has all its entries 0 occurs below
every row which has a non-zero entry.
(ii) The number of zeros before the first non-zero element in a
row is less then the number of such zeros in the next row.
Example 1.6
Find the rank of the matrix A= 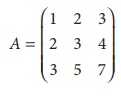
Solution :
The order of A is 3 Ă
3.
⎠Ï(A) †3.
Let us transform the matrix A to an echelon form by using
elementary transformations.

The number of non zero rows is 2
âŽRank of A is 2.
Ï (A) = 2.
Note
A row having atleast one non -zero element is called as non-zero
row.
Example 1.7
Find the rank of the matrix A= 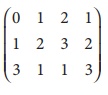
Solution:
The order of A is 3 Ă
4.
âŽ Ï (A)â€3.
Let us transform the matrix A to an echelon form
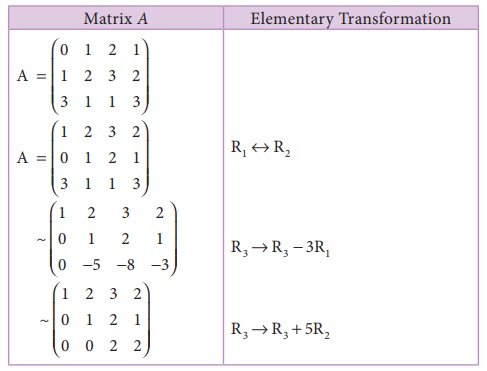
The number of non zero rows is 3. ⎠Ï(A) =3.
Example 1.8
Find the rank of the matrix A= 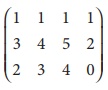
Solution:
The order of A is 3 Ă
4.
⎠Ï(A) †3.
Let us transform the matrix A to an echelon form
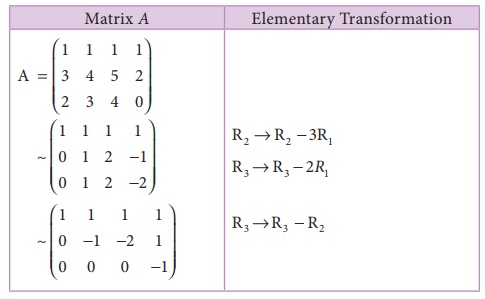
The number of non zero rows is 3.
âŽ Ï (A) =3.
Consistency of Equations
System of linear equations in two variables
We have already studied , how to solve two simultaneous linear
equations by matrix inversion method.
Recall
Linear equations can be written in matrix form AX=B, then the
solution is X = Aâ1B , provided |A| â 0
Consider a system of linear equations with two variables,
ax + by + h
cx + dy + k (1)
Where a, b, c, d, h and k are real constants and neither a and b
nor c and d are both zero.
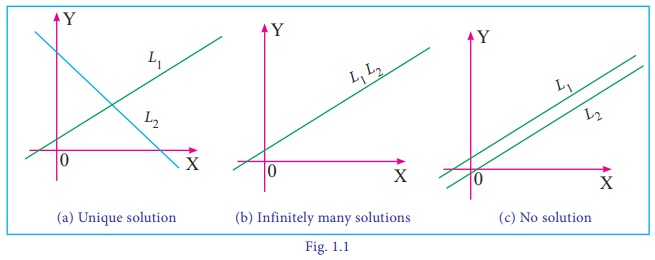
For any tow given lines L1 and L2,
one and only one of the following may occur.
L1 and L2 intersect at exactly one point
L1 and L2 are coincident
L1 and L2 are parallel and distinct.
(see Fig 1.1) In the first case, the system has a unique solution
corresponding to the single point of intersection of the two lines.
In the second case, the system has infinitely many solutions
corresponding to the points lying on the same line
Finally in the third case, the system has no solution because the
two lines do not intersect.
Let us illustrate each of these possibilities by considering some
specific examples.
(a) A system of equations with exactly one solution
Consider the system 2x â
y = 1, 3x + 2 y = 12 which represents two
lines intersecting at (2, 3) i.e (2, 3) lies on both lines. So the equations
are consistent and have unique solution.
(b) A system of equations with infinitely many solutions
Consider the system 2x â
y = 1, 6x â 3y = 3 which represents two
coincident lines. We find that any point on the line is a solution. The
equations are consistent and have infinite sets of solutions such as (0, â1), (1, 1) and so on.
Such a system is said to be dependent.
(c) A system of equations that has no solution
Consider the system 2x â
y = 1, 6x â 3y = 12 which represents two
parallel straight lines. The equations are inconsistent and have no solution.
System of non Homogeneous Equations in three variables
A linear system composed of three linear equations with three
variables x, y and z has the general form
a1 x + b1 y + c1 z = d1
a2 x + b2y + c2z = d2 (2)
a3 x + b3 y + c3 z = d3
A linear equation ax +
by + cz = d (a, b
and c not all equal to zero) in three variables represents a plane in
three dimensional space. Thus, each equation in system (2) represents a plane
in three dimensional space, and the solution(s) of the system is precisely the
point(s) of intersection of the three planes defined by the three linear equations
that make up the system. This system has one and only one solution, infinitely
many solutions, or no solution, depending on whether and how the planes
intersect one another. Figure 1.2 illustrates each of these possibilities.
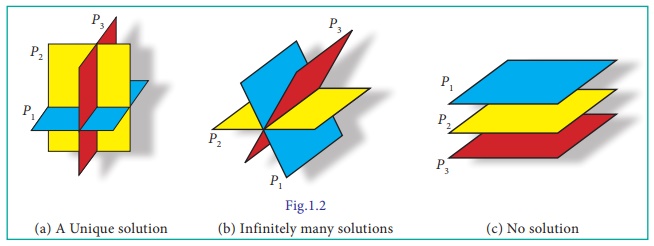
In Figure 1.2(a), the three planes intersect at a point
corresponding to the situation in which system (2) has a unique solution.
Figure 1.2 (b) depicts a situation in which there are infinitely
many solutions to the system. Here the three planes intersect along a line, and
the solutions are represented by the infinitely many points lying on this line.
In Figure 1.2 (c), the three planes are parallel and distinct, so
there is no point in common to all three planes; system (2) has no solution in
this case.
Note
Every system of linear equations has no solution, or has exactly
one solution or has infinitely many
solutions.
An arbitrary system of âmâ linear equations in ânâ
unknowns can be written as
a11 x1 + a 12 x2 + ... + a1n xn =b1
a21 x1 + a 22 x2 + ... + a2n xn =b2
. . ⊠.
.
. . ⊠.
.
. . ⊠.
.
am1 x1 + am 2 x2 + ... + amn xn = bm
where x1, x2,.., xn
are the unknowns and the subscripted aâs and bâs denote the
constants.
Augmented matrices
A system of âmâ linear equations in ânâ unknowns can
be abbreviated by writing only the rectangular array of numbers.
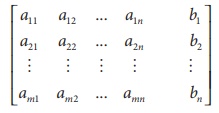
This is called the augmented matrix for the system and 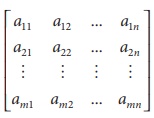 is the coefficient matrix.
is the coefficient matrix.
Consider the following system of equations
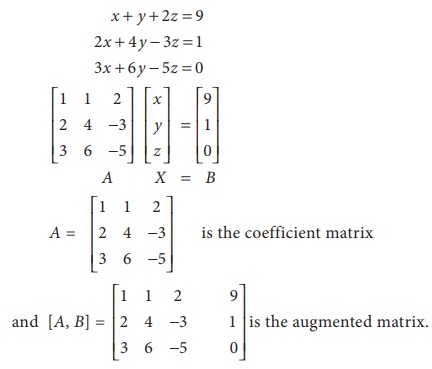
Related Topics