Chapter: Mathematics (maths) : Z-Transforms and Difference Equations
Z-Transforms and Difference Equations
Z-Transforms AND
DIFFERENCE EQUATIONS
1 INTRODUCTION
2 LINEAR DIFFERENCE EQUATIONS
3 Z-TRANSFORMS AND ITS PROPERTIES
4 INVERSE Z-TRANSFORMS
5 CONVOLUTION THEOREM
6 APPLICATIONS OF Z-TRANSFORMS TO
DIFFERENCE EQUATIONS
7 FORMATION OF DIFFERENCE EQUATIONS
1 Introduction
The Z-transform plays a vital role in the field of communication
Engineering and control Engineering, especially in digital signal processing.
Laplace transform and Fourier transform are the most effective tools in the
study of continuous time signals, where as Z –transform is used in discrete
time signal analysis. The application of Z – transform in discrete analysis is
similar to that of the Laplace transform in continuous systems. Moreover,
Z-transform has many properties similar to those of the Laplace transform. But,
the main difference is Z-transform operates only on sequences of the discrete
integer-valued arguments. This chapter gives concrete ideas about Z-transforms
and their properties. The last section applies Z-transforms to the solution of
difference equations.
Difference Equations
Difference
equations arise naturally in all situations in which sequential relation exists
at various discrete values of the independent variables. These equations may be
thought of as the discrete counterparts of the differential equations.
Z-transform is a very useful tool to solve these equations.
A difference
equation is a relation between the independent variable, the dependent
variable and the successive differences of the dependent variable.
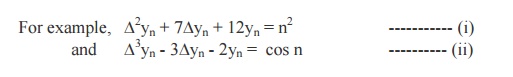
are difference equations.
The differences Dyn, D2yn, etc can
also be expressed as.
Dyn
= yn+1 - yn,
D2yn = yn+2 - 2yn+1 + yn.
D3yn = yn+3 - 3yn+2 + 3yn+1
- yn and so on.
Substituting these in (i)
and (ii), the equations take the form
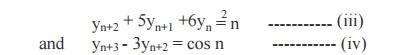
Note that the above
equations are free of Ds¢.
If a difference equation
is written in the form free of Ds,¢then the order of difference equation is the difference between
the highest and lowest subscripts of y‟s occurring in it. For example, the
order of equation (iii) is 2 and equation (iv) is 1.
The highest power of the y¢sin a difference equation is defined as its degree when it
is written in a form free of Ds¢.For example, the degree of the equations yn+3 + 5yn+2
+ yn = n2 + n + 1 is 3 and y3 n+3 +
2yn+1 yn = 5 is 2.
2 Linear Difference
Equations
A linear difference
equation with constant coefficients is of the form
a0 yn+r + a1 yn+r -1
+ a2 yn+r -2 + . . . . +aryn = f(n).
i.e., (a0Er + a1Er-1
+ a2 Er-2 + . . . . + ar)yn = f(n) ------(1)
where a0,a1,
a2, . . . . . ar
are constants and f(n) are known functions of n.
The
equation (1) can be expressed in symbolic form as
f(E) yn
= f(n)
----------(2)
If f(n) is zero, then equation (2) reduces to
f (E) yn
= 0 ----------(3)
which is
known as the homogeneous difference equation corresponding to (2).The
solution of (2) consists of two parts, namely, the complementary function and
the particular integral.
The solution of equation (3) which involves as many arbitrary constants as the order of the equation is called the complementary function. The particular integral is a particular solution of equation(1) and it is a function of „n‟ without any arbitrary constants.
Thus the complete solution of (1) is given by yn = C.F + P.I.
Example 1
Form the difference
equation for the Fibonacci sequence .
The integers
0,1,1,2,3,5,8,13,21, . . . are said to form a Fibonacci sequence.
If yn be the nth
term of this sequence, then
yn = yn-1 + yn-2 for n > 2
or yn+2 - yn+1
- yn = 0 for n > 0
3 Z - Transforms and its
Properties
Definition
Let {fn} be a sequence defined for n = 0,1,2,…….,then its Z-transform F(z) is defined as
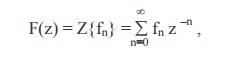
whenever the series
converges and it depends on the sequence {fn}.
The inverse Z-transform of
F(z) is given by Z-1{F(z)} = {fn}.
Note: If {fn}
is defined for
n = 0,
± 1, ±
2, …….,

Properties of Z-Transforms
1.
The Z-transform is linear.
i.e, if F(z) = Z{fn} and G(z) = Z{gn},
then
Z{afn + bgn} = aF(z) + bG(z).


4. If Z{fn}
= F(z), then
Z{fn+k}=
zk{ F(z) –f0 –(f 1 / z ) - … - ( fk-1
/ zk-1) } (k > 0)
Proof

In Particular,
(i) Z{f n+1} = z {F(z) - f0}
(ii) Z{f n+2}= z2 { F(z) –f0 –(f1/z)
}
Corollary
If Z{fn} =
F(z), then Z{fn–k} = z-k F(z).
(5) Initial value Theorem
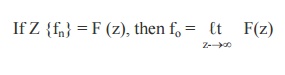
Proof
We know that F (z) = f0 + f1 z-1
+ f2z-2 + . . .
Taking
limits as z ® ¥on both sides, we get
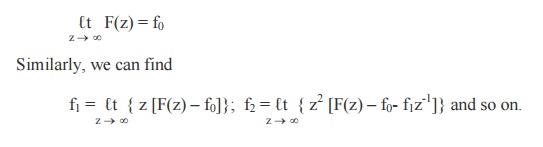
(6) Final
value Theorem

SOME STANDARD RESULTS
1.
Z{an} = z /
(z-a), for |z| > |a|.
Proof
By definition,
we have
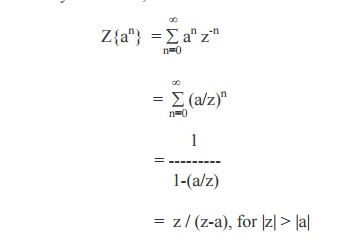
In particular, we have
Z{1} = z / (z-1), (taking a = 1).
and Z{(-1)n} = z / (z +1),
(taking a = -1).
2. Z{nan} = az /(z-a)2
Proof: By property, we have
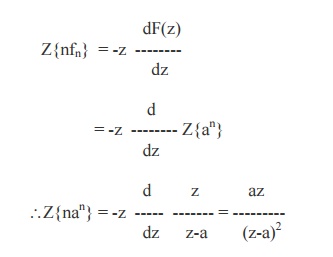
Similarly, we can prove
Z{n2an}
= {az(z+a)}/ (z-a)3

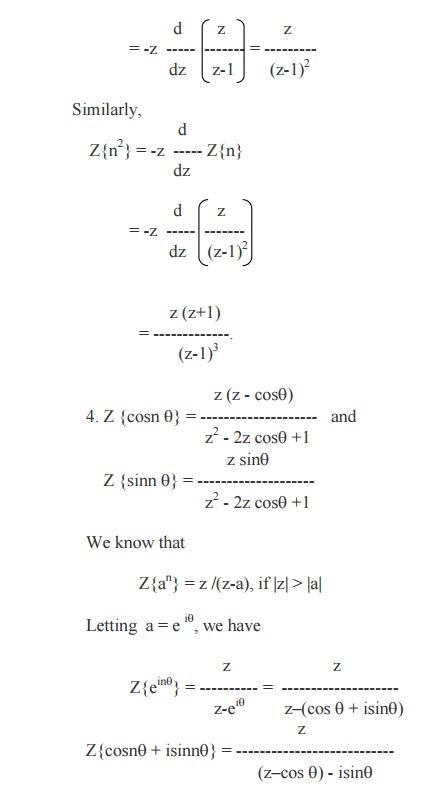
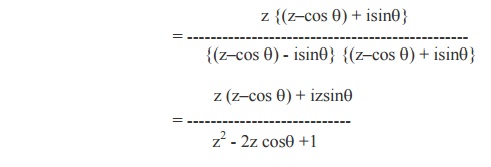
Equating
the Real and Imaginary parts, we get

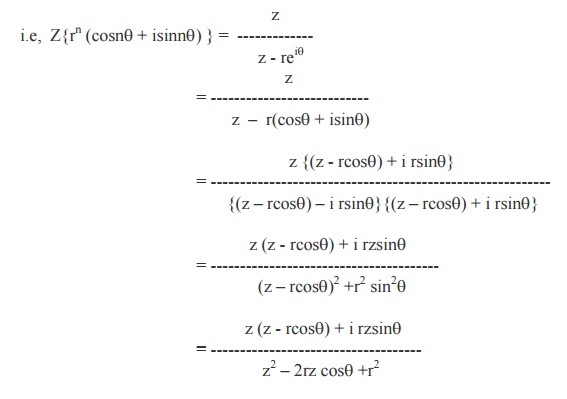
Equating the Real and Imaginary parts, we get
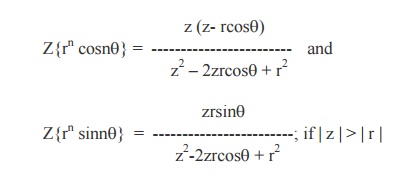
Table of Z –Transforms



Example 2
Find the
Z–transform of
1.
n(n-1)
2.
n2 + 7n + 4
3.
(1/2)( n+1)(n+2)
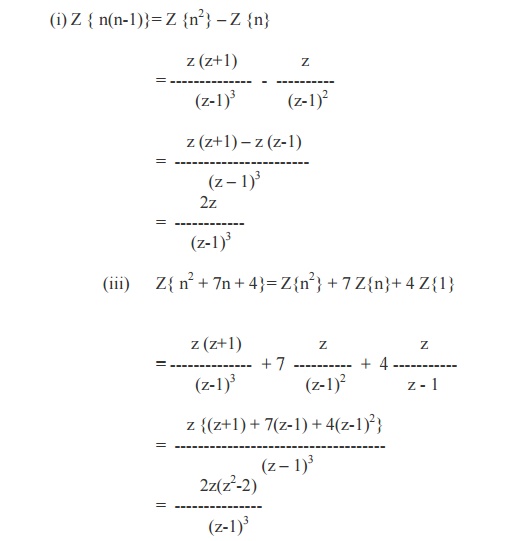
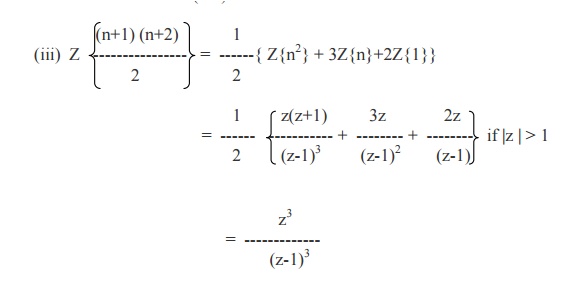
Example 3
Find the
Z- transforms of 1/n and 1/n(n+1)
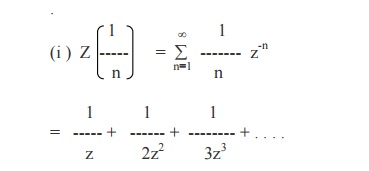
= - log (1 –1/z ) if |1/z|
< 1
= - log (z-1 / z)
=
log (z/z-1), if | z |
>1.

Example 4
Find the Z- transforms of
(i) cos np/2
(ii) sin np/2
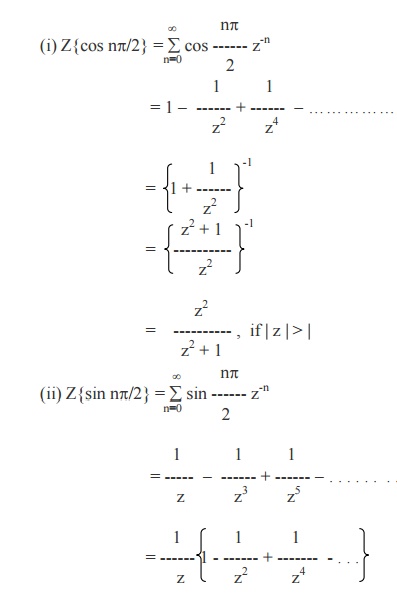

Example 5
Show that
Z{1/ n!} = e1/z and hence find Z{1/ (n+1)!} and Z{1/ (n+2)!}
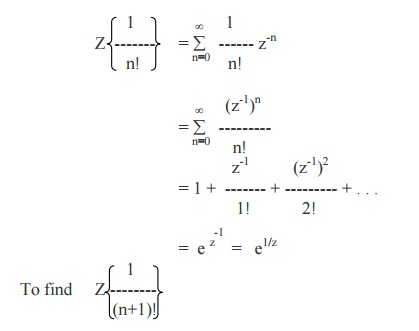
We know that Z{fn+1}
= z { F(z) –f0}
Therefore,
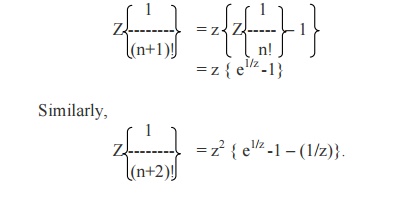
Example 6
Find the
Z- transforms of the following

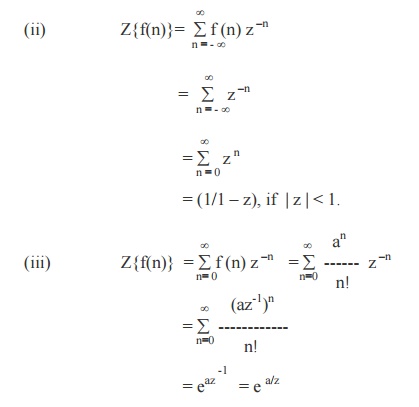

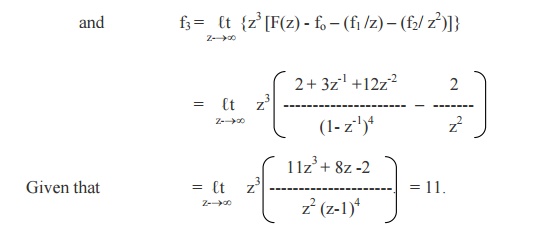
4
Inverse Z –Transforms
The inverse Z –transforms can be obtained by using any one of
the following methods.They are
I.Power
series method
II. Partial
fraction method
III. Inversion
Integral method
IV. Long division method
I. Power
series method
This is
the simplest method of finding inverse Z –transform. Here F(z) can the be
expanded in a series of ascending powers
and the coefficient of z –n will be the of z desired inverse
Z- transform.
Example 8

II. Partial Fraction
Method
Here, F(z) is resolved into partial fractions and the inverse
transform can be taken directly.
Example 9
Find the inverse Z –transform of



Inversion Integral Method or Residue Method
The
inverse Z-transform of F (z) is given by the formula

Sum of
residues of F(z).zn-1 at the poles of F(z) inside the contour C
which is drawn according to the given Region of convergence.
Example
12
Using the
inversion integral method, find the inverse Z-transform of
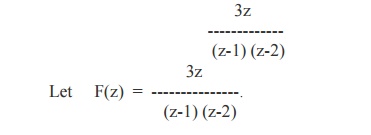
Its poles
are z = 1,2 which are simple poles.
By
inversion integral method, we have
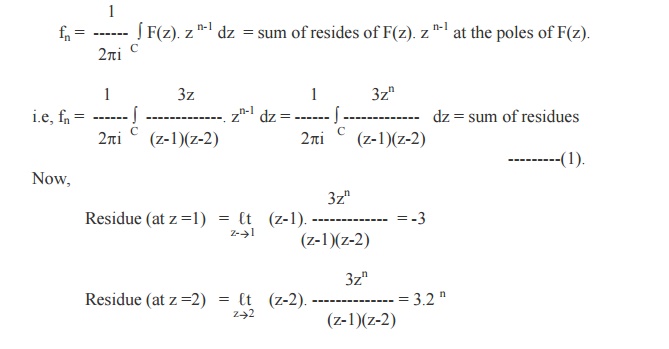
\Sum of Residues = -3 + 3.2n = 3 (2n-1).
Thus the
required inverse Z-transform is
fn
= 3(2n-1), n =
0, 1, 2, …
Example 13
Find the
inverse z-transform of

The pole
of F(z) is z = 1, which is a pole of order 3. By Residue method, we have

IV. Long Division Method
If F(z) is expressed as a ratio of two polynomials, namely, F(z)
= g(z-1) / h(z-1), which can not be factorized, then
divide the numerator by the denominator and the inverse transform can be taken
term by term in the quotient.
Example
14

Thus F(z) = 1 + 3z-1
+ 3z-2 + 3z-3 + . . . . . .
Now,
Comparing the quotient with

Example
15
Find the
inverse Z-transform of


5 CONVOLUTION THEOREM
If Z-1{F (z)} = fn and Z-1{G(z)}
= gn, then

Example
16
Use
convolution theorem to evaluate
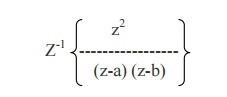
We know
that Z-1 {F(z). G(z)} = fn*gn.
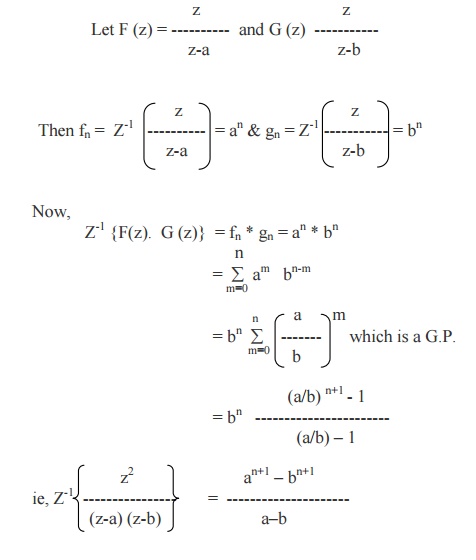

Example 18
Use
convolution theorem to find the inverse Z- transform



6 Application of Z - transform to Difference equations
As we know, the Laplace transforms method is quite effective in
solving linear differential equations, the Z - transform is useful tool in
solving linear difference equations.
To solve a difference equation, we have to take the Z -
transform of both sides of the difference equation using the property
Z{fn+k}= zk{ F(z) –f0 –(f 1
/ z ) - … - ( fk-1 / zk-1) } (k > 0)
Using the initial
conditions, we get an algebraic equation of the form F(z) = f(z).
By taking
the inverse Z-transform, we get the required solution fn of the
given difference equation.
Exmaple 19
Solve the difference equation
yn+1 + yn = 1, y0 = 0, by Z - transform
method.
Given
equation is yn+1 + yn = 1 ---------- (1)
Let Y(z) be the Z
-transform of {yn}.
Taking the Z - transforms
of both sides of (1), we get
Z{yn+1} + Z{yn}
= Z{1}.
ie, z {Y(z) - y0} + Y(z) = z /(z-1).
Using the
given condition, it reduces to
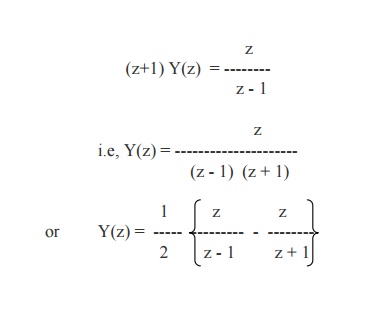
On taking inverse Z-transforms, we obtain
yn
= (1/2){1 - (-1)n}
Example
20
Solve yn+2 + yn = 1, y0 = y1
= 0 , using Z-transforms.
Consider yn+2 + yn = 1 ------------- (1)
Taking Z- transforms on both sides, we get
Z{yn+2}+
Z{yn} = Z{1}

Using Inverse Z-transform, we get
yn =(½){1 - cos (np/ 2) - sin (np/ 2)}.
Example 21
Solve yn+2
+ 6yn+1 + 9yn = 2n, y0 = y1 = 0, using
Z-transforms.
Consider yn+2 + 6yn+1 + 9yn
= 2n -------- (1)
Taking
the Z-transform of both sides, we get
Z{yn+2}
+ 6Z{yn+1} + 9Z{yn} = Z {2n}

On taking Inverse
Z-transforms, we get
yn = (1/ 25){ 2n
- (-3)n + (5/3) n (-3)n}.
Example 22
Solve the simultaneous
equations
xn+1 - yn
= 1; yn+1 - xn = 1 with x (0) = 0; y (0) = 0.
The given equations are
xn+1 - yn
= 1, x0 = 0
yn+1 - xn =1,
y0
= 0 -------------- (2)
Taking
Z-transforms, we get

On taking the inverse Z-transform of both sides, we have xn
= n and yn = n , which is the required solution of the simultaneous
difference equations.
Example
23
Solve xn+1 = 7xn + 10yn
; yn+1 = xn + 4yn,
with x0 = 3, y0 = 2
Given
xn+1
= 7xn + 10yn------------- (1)
yn+1
= xn + 4yn------------- (2)
Taking Z- transforms of
equation(1), we get
z { X(z)
- x0} = 7 X(z) + 10 Y(z)
(z - 7)
X(z) –10 Y(z) = 3z ----------(3)
Again taking Z- transforms
of equation(2), we get
z {Y(z) - y0} = X(z) + 4Y(z)
-X(z)
+ (z - 4)Y(z) = 2z ---------- (4)
Eliminating
„x‟
from (3) &
(4), we get

Taking Inverse Z-transforms, we get
yn = 9n + 2n.
From (2),
xn = yn+1 - 4yn = 9n+1 + 2n+1 - 4 (9n
+ 2n)
= 9.9n + 2.2n - 4.9n - 4.2n
Therfore,
xn = 5.9n - 2.2n
Hence the
solution is xn = 5.9n
- 2.2n and yn = 9n + 2n.
Exercises
Solve the
following difference equations by Z –transform method
1. yn+2 + 2yn+1 + yn = n, y0 = y1 = 0
2. yn+2 –yn = 2n, y0
= 0, y1 = 1
3. un+2 –2cosaun+1+ un=0, u0 = 1, u1
= cosa
4. un+2 = un+1 + un, u0
= 0, u1 = 1
5. yn+2 –5yn+1+ 6yn = n (n-1), y0
= 0, y1 = 0
6. yn+3 –6yn+2 + 12yn+1 –8yn
= 0, y0 = -1, y1 = 0, y2 = 1
7 FORMATION OF DIFFERENCE EQUATIONS
Example
Form
the difference equation
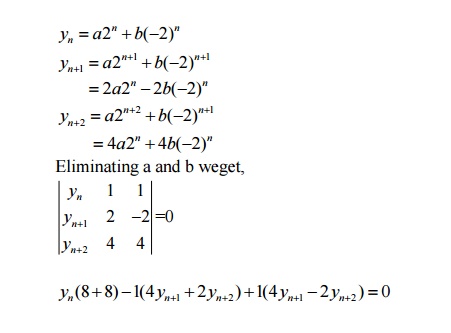
16 y n -4 yn+2 =0
-4( y n +2 -4yn ) =0
y n +2 -4 yn =0
Exercise:
1.
Derive the difference equation form yn
=( A +Bn)( 3)-n
2.
Derive the difference equation form U
n =A2n
+Bn
Related Topics