Important Questions and Answers: Z-Transforms and Difference Equations

Z -TRANSFORMS AND DIFFERENCE EQUATIONS

PART –A

1 =A(n+1)+B(n)

Put n =0 we get, 1 =A

Put n =-1 we get, 1 =-B  (i.e) B =-1

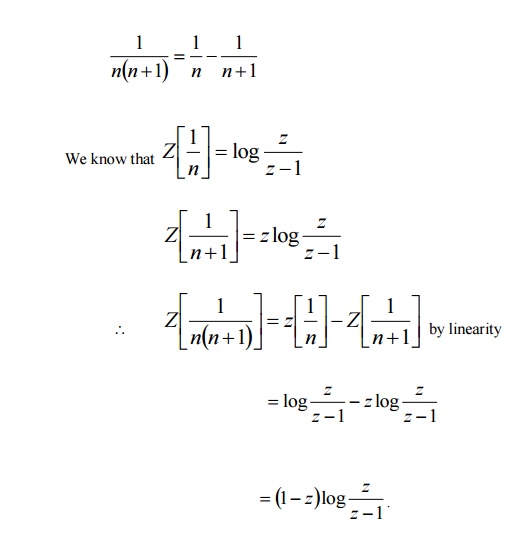
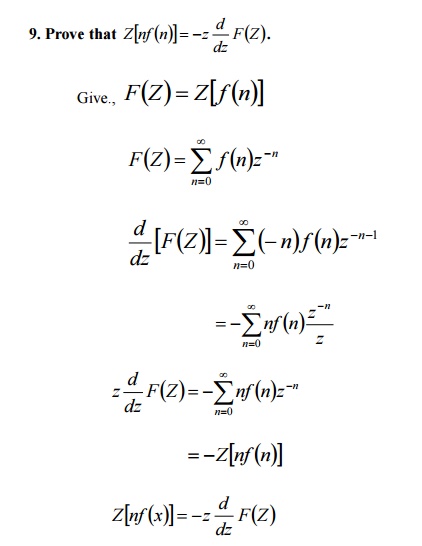
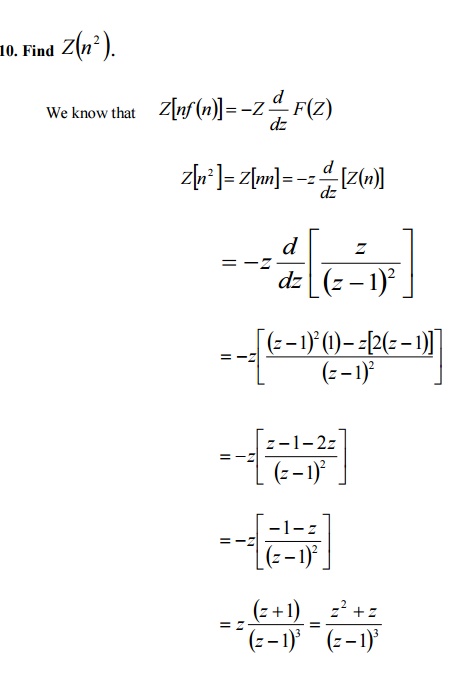
11. Find the Z-transform of {nCk }.

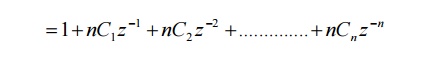
This is the expansion of binominal theorem.

=(1+z -1 )n

12. Find Z[e-tt 2 ].

We know that  Z[e-at f (t)]=Z[f(t)]z®zeaT

Z[e-tt 2 ]=[Z[t2 ]z®zeT

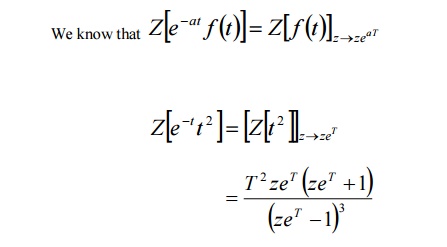
13. Define Unit Sample sequence.

The unit sample sequence d(n)is defined the sequence with values

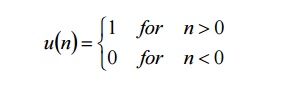
14. Define Unit step sequence.

The unit step sequence u(n)has values.

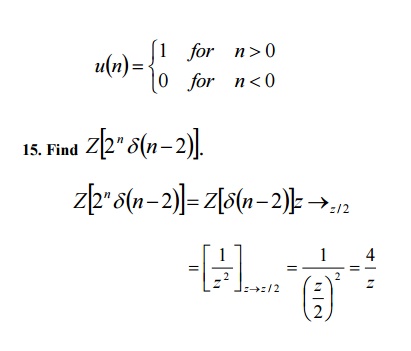
16. If Z[f(n)]=F(z),, then 

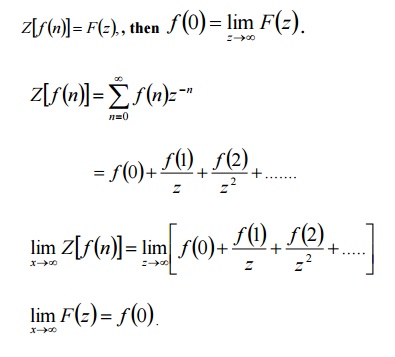
17. Find the Z-transform of na n u(n).

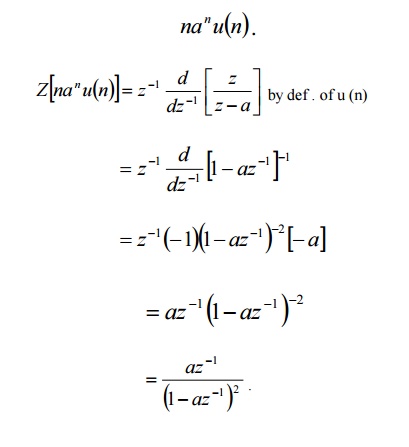
18.   Define convolution of sequences. 

i) The convolution of two sequences  {x(n)}and {y(n)}is defined as 

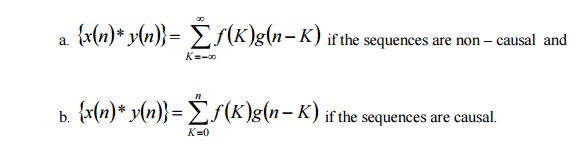
ii)The convolution of two functions f(t) and g (t) is defined as

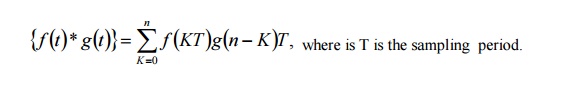
Introduction

The Z-transform plays a vital role in the field of communication Engineering and control Engineering, especially in digital signal processing. Laplace transform and Fourier transform are the most effective tools in the study of continuous time signals, where as Z –transform is used in discrete time signal analysis. The application of Z – transform in discrete analysis is similar to that of the Laplace transform in continuous systems. Moreover, Z-transform has many properties similar to those of the Laplace transform. But, the main difference is Z-transform operates only on sequences of the discrete integer-valued arguments. This chapter gives concrete ideas about Z-transforms and their properties. The last section applies Z-transforms to the solution of difference equations.