Inverse Z-Transforms

Inverse Z –Transforms

The inverse Z –transforms can be obtained by using any one of the following methods.They are

I.Power series method

II. Partial fraction method

III.  Inversion Integral method

IV.  Long division method

I. Power series method

This is the simplest method of finding inverse Z –transform. Here F(z) can the be expanded in a series of ascending powers  and the coefficient of z –n will be the of z desired inverse Z- transform.

Example 8

 Find the inverse Z –transform of log {z /(z+1)} by power series method.

II. Partial Fraction Method

Here, F(z) is resolved into partial fractions and the inverse transform can be taken directly.

Example 9

Find the inverse Z –transform of 

Inversion Integral Method or Residue Method

The inverse Z-transform of F (z) is given by the formula

Sum of residues of F(z).zn-1 at the poles of F(z) inside the contour C which is drawn according to the given Region of convergence.

Example 12

Using the inversion integral method, find the inverse Z-transform of

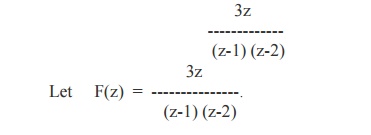
Its poles are z = 1,2 which are simple poles.

By inversion integral method, we have

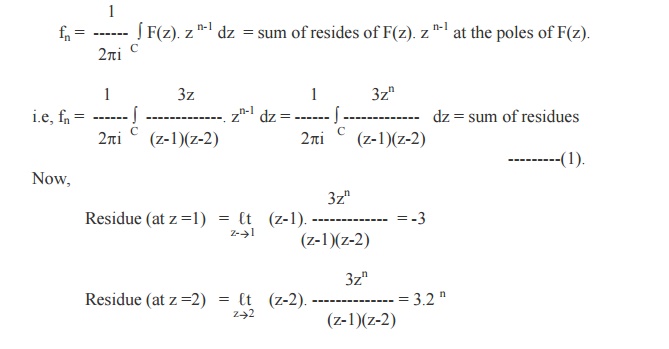
\Sum of Residues = -3 + 3.2n = 3 (2n-1).

Thus the required inverse Z-transform is

fn = 3(2n-1),   n   =   0,   1,   2,   …

Example 13

Find the inverse z-transform of 

The pole of F(z) is z = 1, which is a pole of order 3. By Residue method, we have

IV. Long Division Method

If F(z) is expressed as a ratio of two polynomials, namely, F(z) = g(z-1) / h(z-1), which can not be factorized, then divide the numerator by the denominator and the inverse transform can be taken term by term in the quotient.

Example 14

Thus F(z) = 1 + 3z-1 + 3z-2 + 3z-3 + . . . . . .

Now, Comparing the quotient with

Example 15

Find the inverse Z-transform of