Application of Z - transform to Difference equations

Application of Z - transform to Difference equations

As we know, the Laplace transforms method is quite effective in solving linear differential equations, the Z - transform is useful tool in solving linear difference equations.

To solve a difference equation, we have to take the Z - transform of both sides of the difference equation using the property

Z{fn+k}= zk{ F(z) –f0 –(f 1 / z ) - … - ( fk-1 / zk-1) } (k > 0)

Using the initial conditions, we get an algebraic equation of the form F(z) = f(z).

By taking the inverse Z-transform, we get the required solution fn of the given difference equation.

Exmaple 19

Solve the difference equation  yn+1 + yn = 1, y0 = 0, by Z - transform method.

Given equation is yn+1 + yn = 1                         ---------- (1)

Let Y(z) be the Z -transform of {yn}.

Taking the Z - transforms of both sides of (1), we get

Z{yn+1} +  Z{yn} = Z{1}.

ie, z {Y(z) - y0} + Y(z) = z /(z-1).

Using the given condition, it reduces to

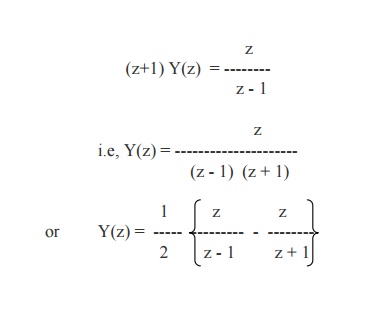
On taking inverse Z-transforms, we obtain

yn = (1/2){1 - (-1)n}

Example 20

Solve         yn+2       + yn = 1, y0 = y1 = 0 ,     using Z-transforms.

Consider      yn+2       + yn = 1   -------------       (1)

Taking Z- transforms on both sides, we get

Z{yn+2}+ Z{yn} = Z{1}

Using Inverse Z-transform, we get

yn =(½){1 - cos (np/ 2) - sin (np/ 2)}.

Example 21

Solve yn+2 + 6yn+1 + 9yn = 2n,  y0 = y1 = 0, using Z-transforms.

Consider yn+2 + 6yn+1 + 9yn = 2n -------- (1)

Taking the Z-transform of both sides, we get

Z{yn+2} + 6Z{yn+1} + 9Z{yn} = Z {2n}

On taking Inverse Z-transforms, we get

yn = (1/ 25){ 2n - (-3)n + (5/3) n (-3)n}.

Example 22

Solve the simultaneous equations

xn+1 - yn = 1; yn+1 - xn = 1 with x (0) = 0; y (0) = 0.

The given equations are

xn+1 - yn = 1, x0 = 0

yn+1 - xn  =1,

y0 = 0   -------------- (2)

Taking Z-transforms, we get

On taking the inverse Z-transform of both sides, we have xn = n and yn = n , which is the required solution of the simultaneous difference equations.

Example 23

Solve xn+1 = 7xn + 10yn ;  yn+1 = xn + 4yn, with x0 = 3, y0 = 2

Given

xn+1 = 7xn + 10yn------------- (1) 

yn+1 = xn + 4yn------------- (2)

Taking Z- transforms of equation(1), we get

z { X(z) - x0} = 7 X(z) + 10 Y(z)

(z - 7) X(z) –10 Y(z) = 3z ----------(3)

Again taking Z- transforms of equation(2), we get

z {Y(z) - y0} = X(z) + 4Y(z)

-X(z) + (z - 4)Y(z) = 2z ----------        (4)

Eliminating „x‟   from   (3)   &   (4),   we   get 

Taking Inverse Z-transforms, we get 

yn = 9n + 2n.

From (2), xn = yn+1 - 4yn  = 9n+1 + 2n+1 - 4 (9n + 2n)

= 9.9n + 2.2n - 4.9n - 4.2n

Therfore, xn = 5.9n - 2.2n

Hence the solution is  xn = 5.9n - 2.2n   and  yn = 9n + 2n.

Exercises

Solve the following difference equations by Z –transform method

1. yn+2 + 2yn+1 + yn = n,  y0 = y1 = 0

2. yn+2 –yn = 2n, y0 = 0, y1 = 1

3. un+2 –2cosaun+1+ un=0, u0 = 1, u1 = cosa

4. un+2 = un+1 + un, u0 = 0, u1 = 1 

5. yn+2 –5yn+1+ 6yn = n (n-1), y0 = 0, y1 = 0 

6. yn+3 –6yn+2 + 12yn+1 –8yn = 0, y0 = -1, y1 = 0, y2 = 1