Fourier Transforms and its properties

Fourier Transforms and its properties

Fourier Transform

We know that the complex form of Fourier integral is

The function F(s), defined by (1), is called the Fourier Transform of f(x). The function f(x), as given by (2), is called the inverse Fourier Transform of F(s). The equation (2) is also referred to as the inversion formula.

Properties of Fourier Transforms

(1) Linearity Property

If  F(s) and G(s) are Fourier Transforms of f(x) and g(x) respectively, then

F{a f(x) + bg(x)} = a F(s) + bG(s),

where a and b are constants.

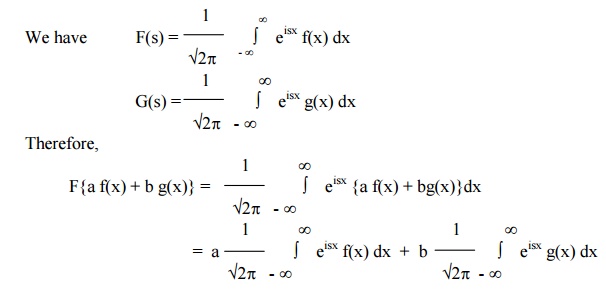
= a F(s) + bG(s) i.e,

F{a f(x) + bg(x)} = a F(s) + bG(s)

(2) Shifting Property 

(i)                If  F(s) is the complex Fourier Transform of f(x), then 

F{f(x-a)} = eisa F(s).

(ii) If F(s) is the complex Fourier Transform of f(x), then

(3) Change of scale property

If F(s) is the complex Fourier transform of f(x), then

F{f(ax)} =1/a F(s/a), a ¹0.

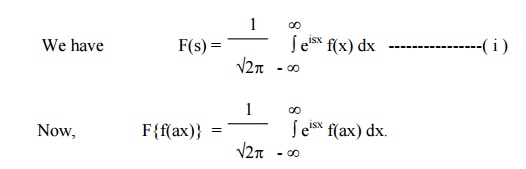
Put  ax = t, so that dx = dt/a.

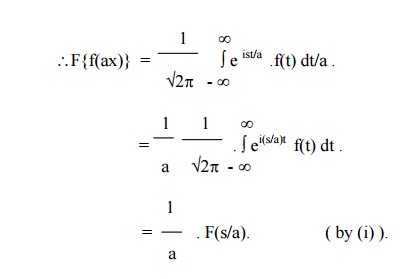
(4) Modulation theorem.

If F(s) is the complex Fourier transform of f(x),

Then  F{f(x) cosax} = ½{F(s+a) + F(s-a)}.

(5) nth derivative of the Fourier Transform

If F(s) is the complex Fourier Transform of f(x),

Then F{xn f(x)} = (-i)n dn/dsn .F(s).

(6) Fourier Transform of the derivatives of a function.

If  F(s) is the complex Fourier Transform of f(x),

Then, F{f-isF(s) if„(x)}f(x)®0as x=® ±¥.

In general, the Fourier transform of the nth derivative of f(x) is given by

F{f n(x)} = (-is)n F(s),

provided-1 ‟the derivatives frst®„n±¥.   vanish   as   x

Property (7)

If F(s) is the complex Fourier Transform of f(x), then F 

Property (8)

If F(s) is the complex Fourier transform of f(x),

Note:  If F{f(x)} = F(s), then

F{f(-x)} = F(-s).

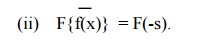
Example 1

Find the F.T of f(x) defined by

f(x) = 0       x<a

= 1    a<x<b

= 0    x>b.

The F.T of f(x) is given by

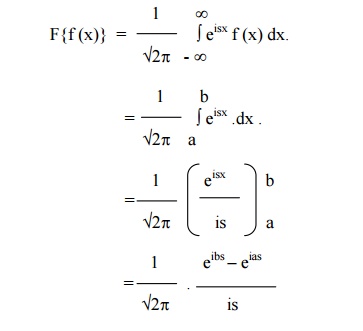
Example 2

Find the F.T of f(x) = x  for  |x | =< a

= 0    for |x | > a.

Example 3

Find the F.T of   f(x) = eiax ,  0 < x < 1

= 0 otherwise

The F.T of f(x) is given by

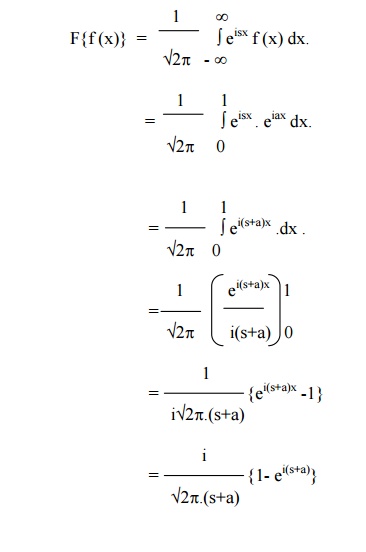
Note:

If the F.T of f(x) is f(s), the function f(x) is called self-reciprocal. In the above example e -x 2/ 2 is self-reciprocal under F.T.

Example 5

Find the F.T of               

f(x) = 1 for |x|<1.

= 0 for |x|>1.